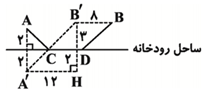
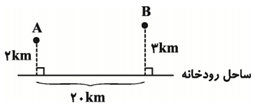
مطابق شكل دو شهر $A$ و $B$ مفروض‌اند. می‌خواهيم جاده‌ای از $A$ به $B$ بسازيم، به طوری كه 8 كيلومتر از اين جاده در ساحل رودخانه ساخته شود. اندازهٔ كوتاه‌ترين مسير ممكن برای اين جاده چند كيلومتر است؟
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...