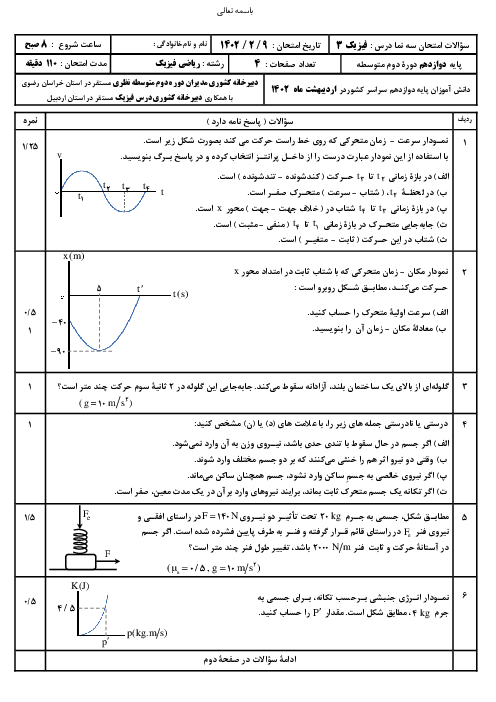
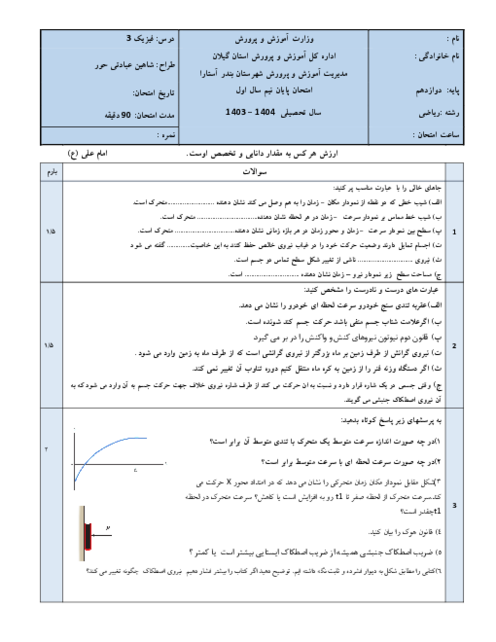
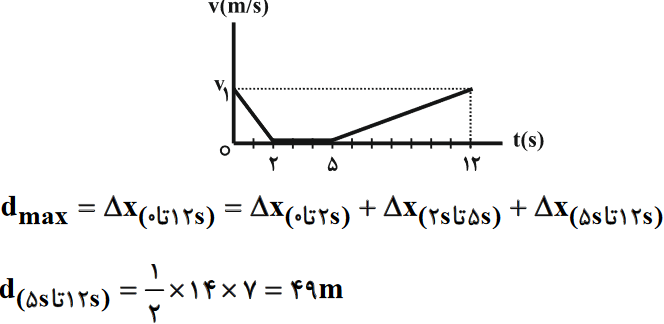قسمت 3: حرکت با شتاب ثابت
فیزیک (3) ریاضی
دوازدهم
متوسطه دوم نظری
علوم ریاضی
درسنامه آموزشی این مبحث
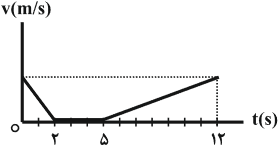
متحرکی در راستای خط راست در حال حرکت است و نمودار سرعت - زمان آن به صورت زیر است. اگر بیشترین فاصلهٔ متحرک از مبدأ حرکت تا لحظهٔ $t=12s$ برابر با $63m$ باشد، مسافت طی شده توسط آن در مرحلهٔ تندشونده چند متر خواهد بود؟