درس 2: معادلهٔ درجهٔ دوم و تابع درجه 2
ریاضی (2)
یازدهم
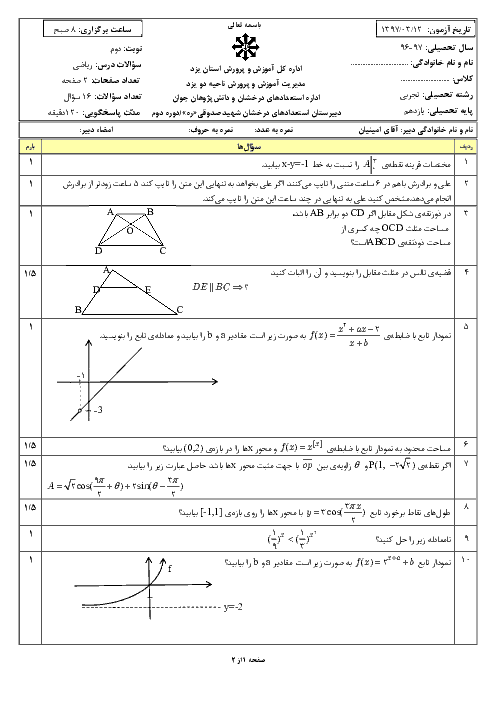
متوسطه دوم نظری
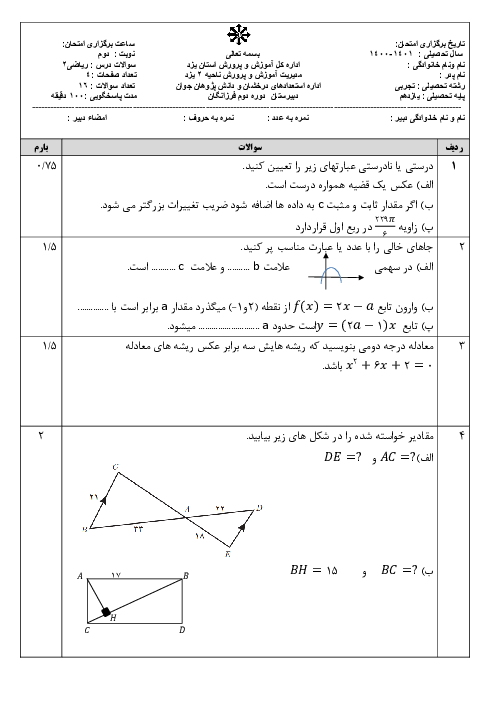
علوم تجربی
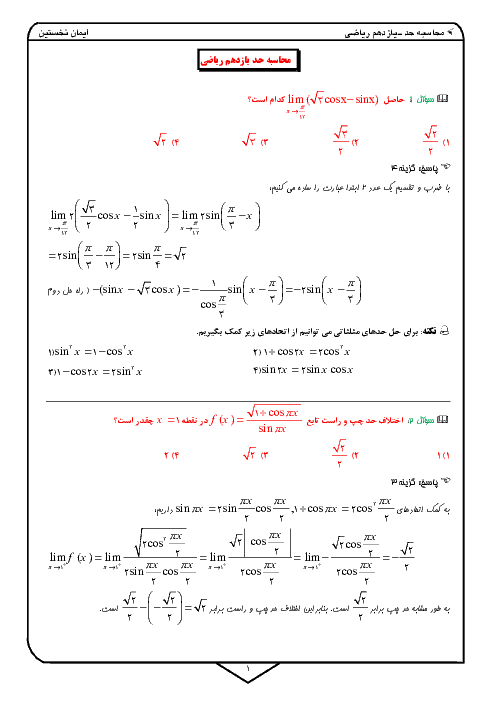
درسنامه آموزشی این مبحث
اگر محور تقارن سهمی به معادلهٔ $y={{x}^{2}}-kx+1$ به صورت $x=-2$ باشد، کمترین مقدار سهمی کدام است؟