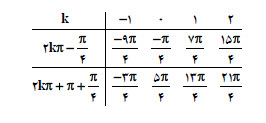نكته: جواب كلي معادلۀ $\operatorname{sinx}=\operatorname{sina}$ برابر با $x=\left( 2k+1 \right)\pi -a,x=2k\pi +a$ است که $k\in z$.

چون: $\frac{5\pi }{4}$ جواب معادله است، پس در معادله صدق می‌كند. بنابراين:

$a\sin \frac{5\pi }{4}+\sqrt{8}=0\Rightarrow a\times \left( \frac{-\sqrt{2}}{2} \right)+2\sqrt{2}=0\Rightarrow -\frac{a}{2}=-2\Rightarrow a=4$ 

\[4\operatorname{sinx}+\sqrt{8}=0\Rightarrow \operatorname{sinx}=\frac{-2\sqrt{2}}{4}\Rightarrow \operatorname{sinx}=\frac{-\sqrt{2}}{2}\Rightarrow \operatorname{sinx}=\sin \left( -\frac{\pi }{4} \right)\Rightarrow \left\{ \begin{matrix}    x=2k\pi -\frac{\pi }{4}  \\    x=2k\pi +\pi +\frac{\pi }{4}  \\ \end{matrix} \right.\left( k\in z \right)\] 

حال با جای گذاری مقادير مختلف $k$ ، جواب‌های مختلف معادله را به دست می‌آوريم: 

مطابق جدول بالا، اولين جواب معادله كه بزرگ‌تر از $\frac{5\pi }{4}$ باشد، $\frac{7\pi }{4}$ است.