درس 2: تابع درجه سوم، توابع یکنوا و بخش‌پذیری و تقسیم
حسابان (2)
دوازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
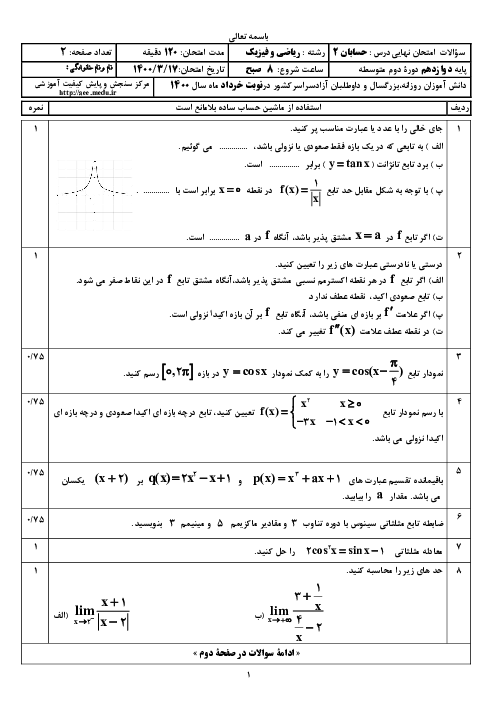
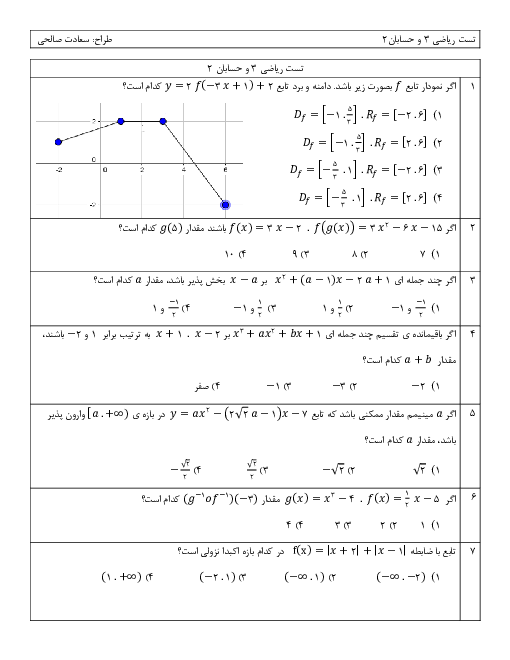
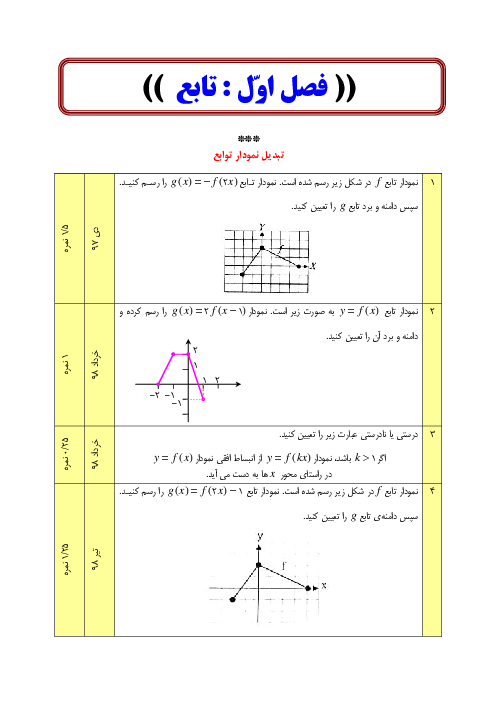
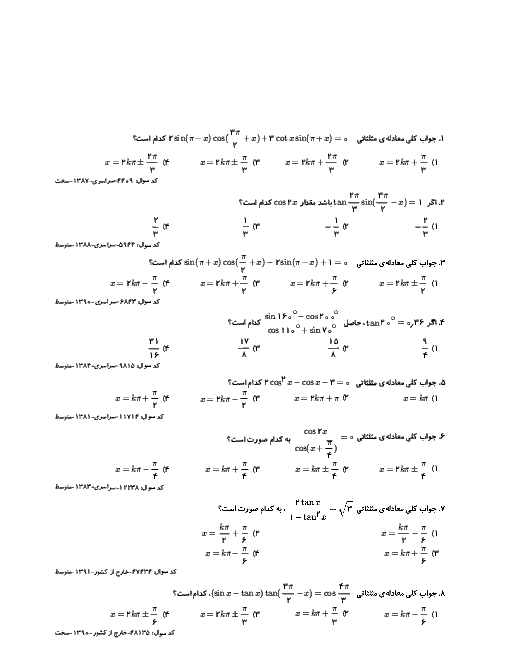اگر تابع $f=\left\{ (-1,a-1),(0,{{a}^{3}}-1),(-2,a) \right\}$ اکیداً نزولی باشد، حدود $a$ کدام است؟
1 )
$\left( -\infty ,0 \right)\bigcup \left( 1,+\infty \right)$
2 )
$\left( -\infty ,-1 \right)\bigcup \left( 1,+\infty \right)$
3 )
$\left( -\infty ,0 \right)\bigcup \left( 0,1 \right)$
$\left( -\infty ,-1 \right)\bigcup \left( 0,1 \right)$
پاسخ تشریحی :
تحلیل ویدئویی تست
عباس ابراهیمی علویجه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...