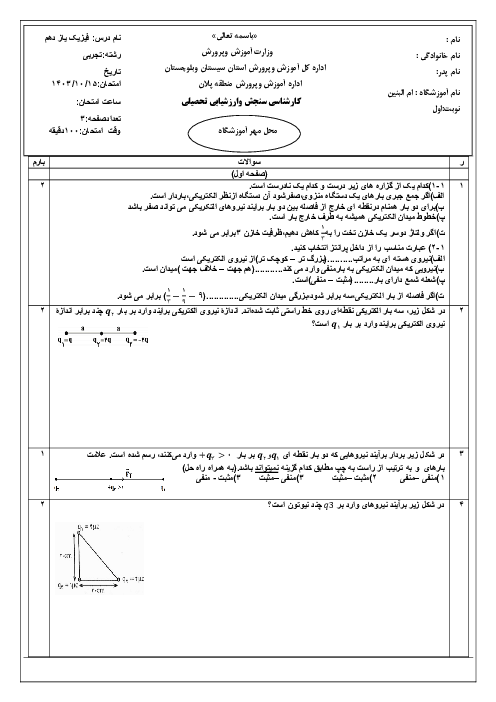
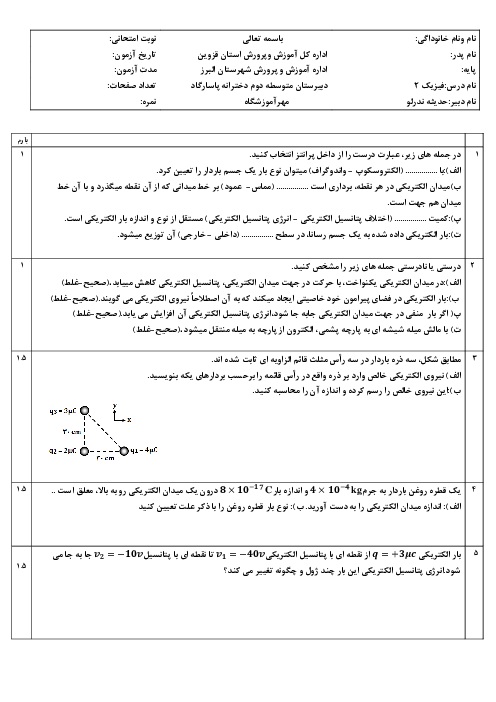
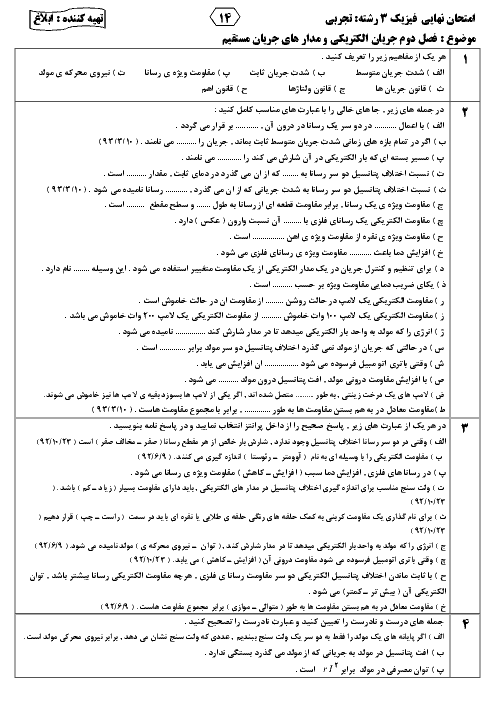
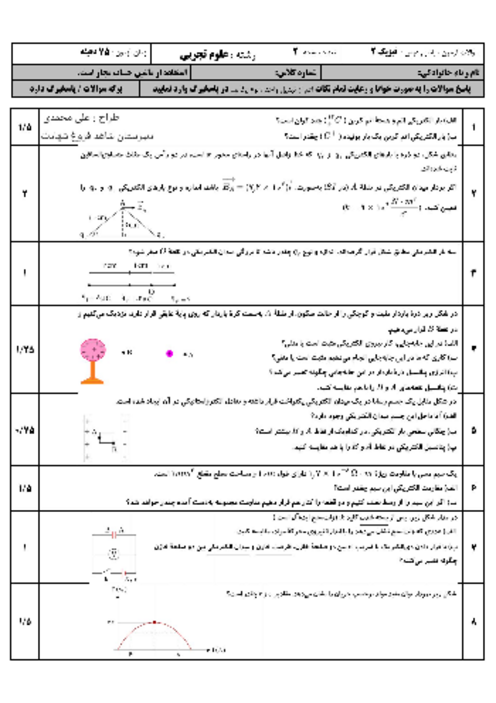
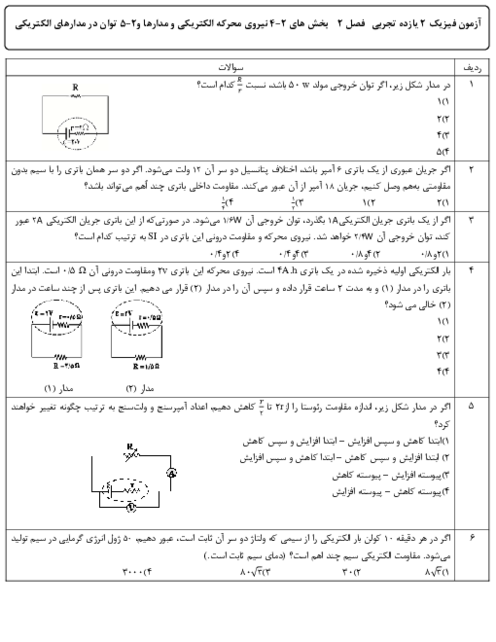
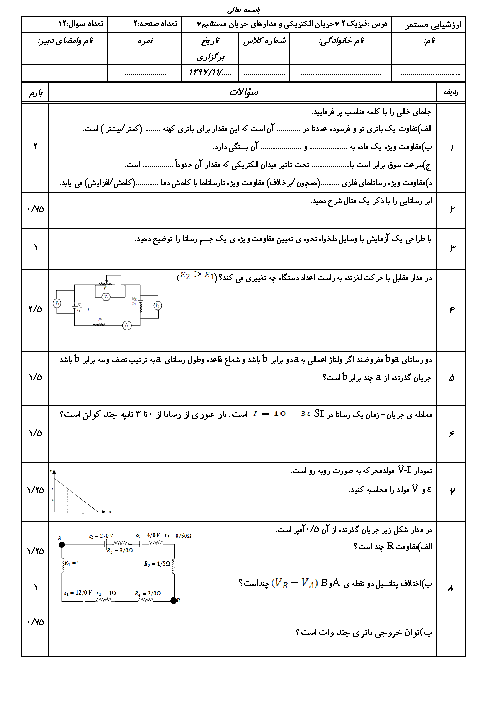
با توجه به شکل ابتدا فاصلهٔ بار ${{q}_{3}}$ را تا دو بار دیگر به‌دست می‌آوریم:

$\begin{align}
  & \sin {{37}^{{}^\circ }}=\frac{\overline{AB}}{\overline{AC}}\Rightarrow 0/6=\frac{\overline{AB}}{20}\Rightarrow \overline{AB}=12cm \\
 & \cos {{37}^{{}^\circ }}=\frac{\overline{BC}}{\overline{AC}}\Rightarrow 0/8=\frac{\overline{BC}}{20}\Rightarrow \overline{BC}=16cm \\
\end{align}$
$F=k\frac{\left| q \right|\left| {{q}_{3}} \right|}{{{r}^{2}}}\Rightarrow \left\{ \begin{matrix}
   {{F}_{13}}=9\times {{10}^{9}}\times \frac{3\times {{10}^{-6}}\times 16\times {{10}^{-6}}}{{{(12\times {{10}^{-2}})}^{2}}}=30N  \\
   {{F}_{23}}=9\times {{10}^{9}}\times \frac{8\times {{10}^{-6}}\times 16\times {{10}^{-6}}}{{{(16\times {{10}^{-2}})}^{2}}}=45N  \\
\end{matrix}\Rightarrow {{F}_{T}}=\sqrt{F_{13}^{2}+F_{23}^{2}} \right.=\sqrt{{{30}^{2}}+{{45}^{2}}}=15\sqrt{13}N$