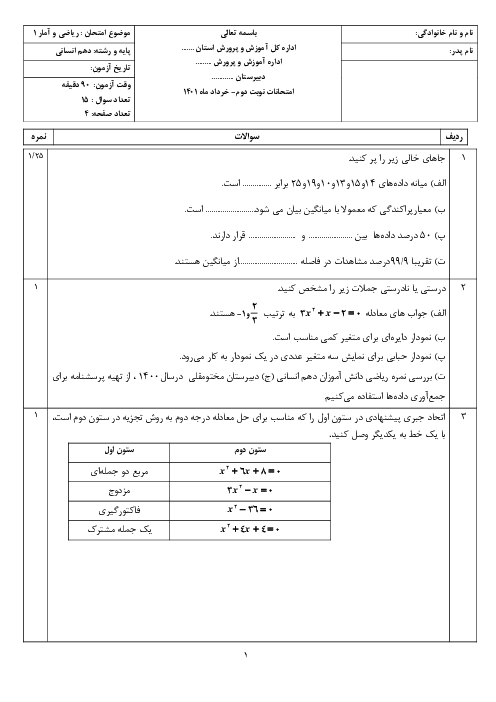
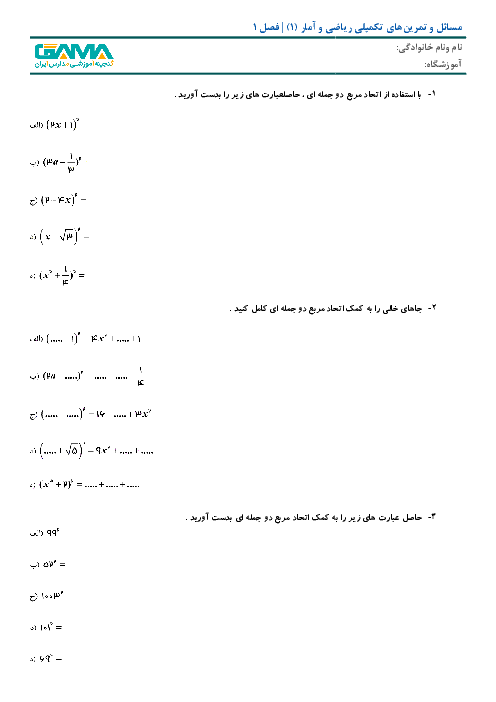
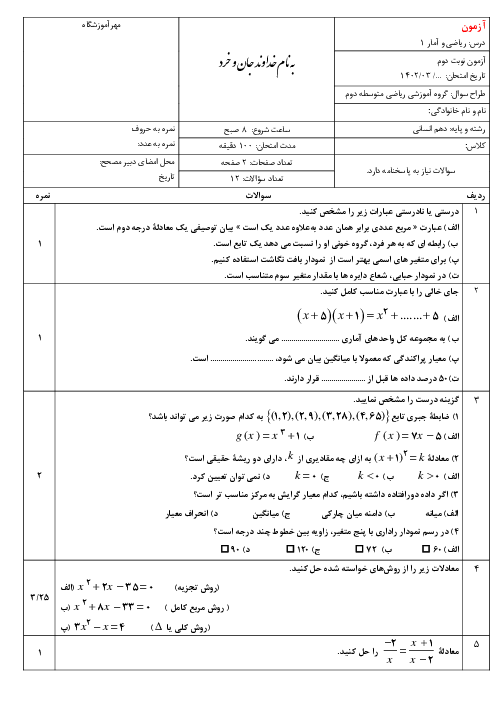
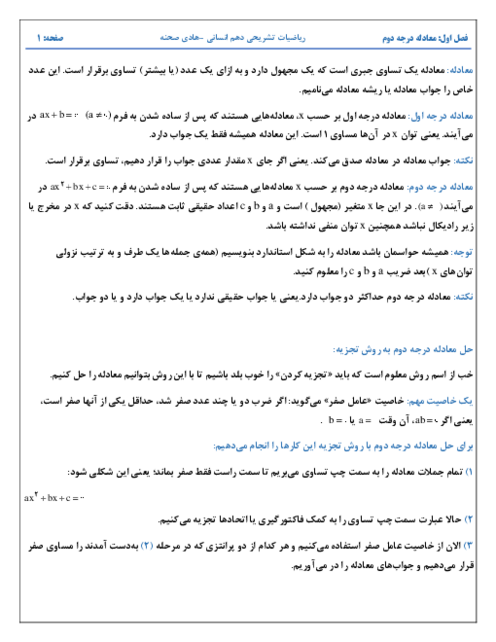
درس 3: معادلههای شامل عبارتهای گویا
ریاضی و آمار (1)
دهم
متوسطه دوم نظری
ادبیات و علوم انسانی
درسنامه آموزشی این مبحث
دو کارگر وقتی با هم کار میکنند، کاری را در 6 روز انجام میدهند، ولی اگر به تنهایی کار کنند، کارگر اول باید 5 روز بیشتر از کارگر دوم کار کند تا کار تمام شود، کارگر دوم کار را در چند روز به اتمام میرساند؟