حدود کدام باشد تا تابع یک تابع صعودی باشد؟ | ریاضی (3) دوازدهم شماره 71933

گاما رو نصب کن!

برای استفاده بسیاری از امکانات گاما و خیلی از وبسایت ها باید جاوا اسکریپت را در مرورگر خود فعال کنید.

برای این کار باید به تنظیمات مرورگر خود مراجعه کنید.

جستجو

پربازدیدها: #{{ tag.title }}

نمونه سوال

فایل آموزشی

پرسش و پاسخ

آزمون آنلاین

درسنامه آموزشی

مدرسه یاب

جستجوهای پرتکرار

ریاضی پنجم فصل اول ریاضی ششم فصل اول الگوی مثلثی عدد شش رقمی بدون تکرار تغییر فیزیکی و شیمیایی ریاضی چهارم خط به خط زیست دهم جمله خبری نهاد چیست چه اعدادی بر ۶ بخش پذیرند مسند چیست مراحل روش علمی درس اول زبان هشتم با معنی و تلفظ

نمونه سوال

محتوای آموزشی

آزمون آنلاین

پرسش و پاسخ

درسنامه آموزشی

مدرسه یاب

معلم خصوصی

درس 1: توابع چند جمله‌ای- توابع صعودی و نزولی ریاضی (3) دوازدهم دوره دوم متوسطه- نظری علوم تجربی درسنامه آموزشی این مبحث

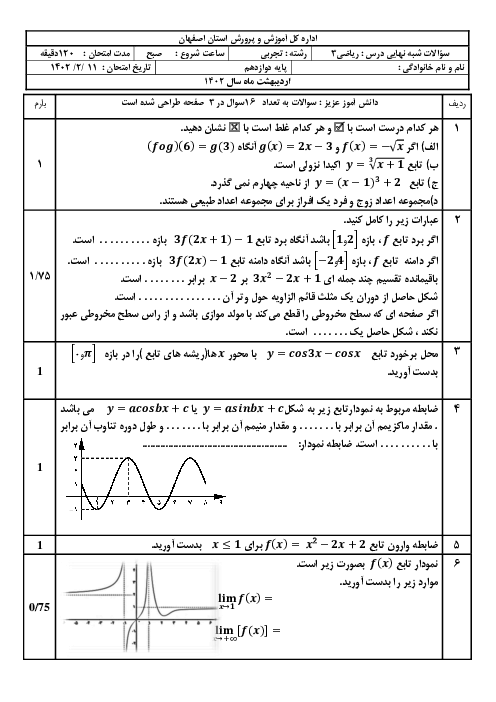
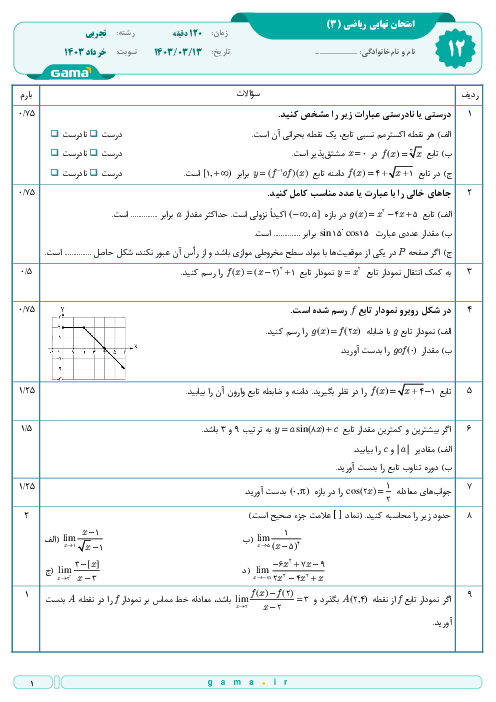
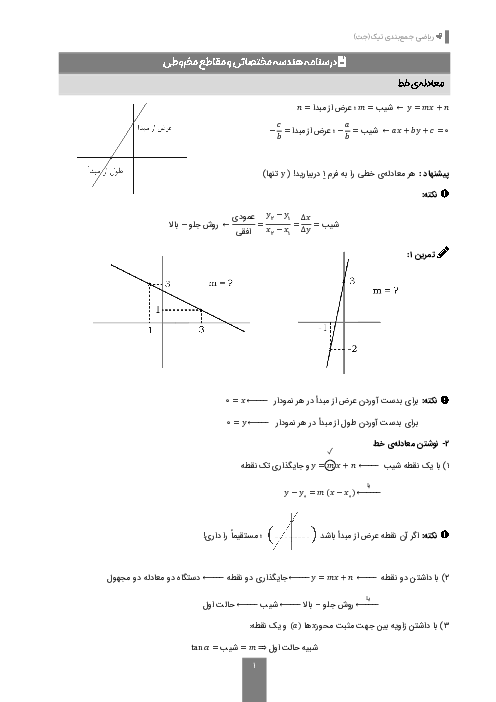
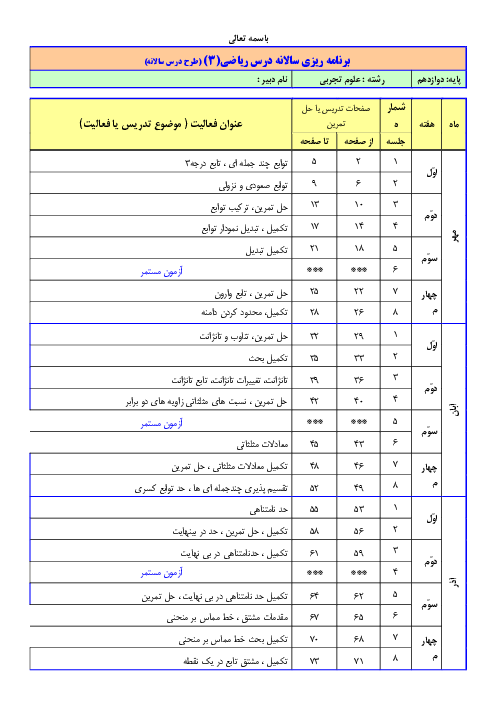
حدود $m$ کدام باشد تا تابع $f=\left\{ (5,6),(3,{{m}^{2}}-m),(-4,2),(4,{{m}^{2}}-m) \right\}$ یک تابع صعودی باشد؟

1 )

$\left( -2,1 \right)\bigcup \left( 2,3 \right)$

2 )

$\left[ -2,1 \right]\bigcup{\left[ 2,3 \right]}$

3 )

$\left[ -2,3 \right]-\left[ -1,2 \right]$

4 )

$\left[ -2,3 \right]-\left( -1,2 \right)$

نمایش پاسخ

باتوجه به صعودی بودن تابع $f$ داريم:

$2\le {{m}^{2}}-m={{m}^{2}}-m\le 6\Rightarrow 2\le {{m}^{2}}-m\le 6$

$\Rightarrow \left\{ \begin{matrix} {{m}^{2}}-m\ge 2\Rightarrow {{m}^{2}}-m-2\ge 0\Rightarrow m\in \left( -\infty ,-1 \right]\bigcup \left[ 2,+\infty \right)(1) \\ {{m}^{2}}-m\le 6\Rightarrow {{m}^{2}}-m-6\le 0\Rightarrow m\in \left[ -2,3 \right](2) \\ \end{matrix} \right.$

$\xrightarrow{(1)\bigcap (2)}\left[ -2,-1 \right]\bigcup \left[ 2,3 \right]=\left[ -2,3 \right]-(-1,2)$