قسمت 3: حرکت با شتاب ثابت
فیزیک (3) ریاضی
دوازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
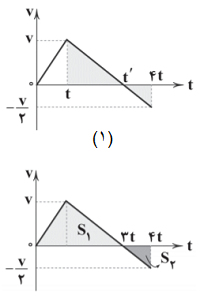
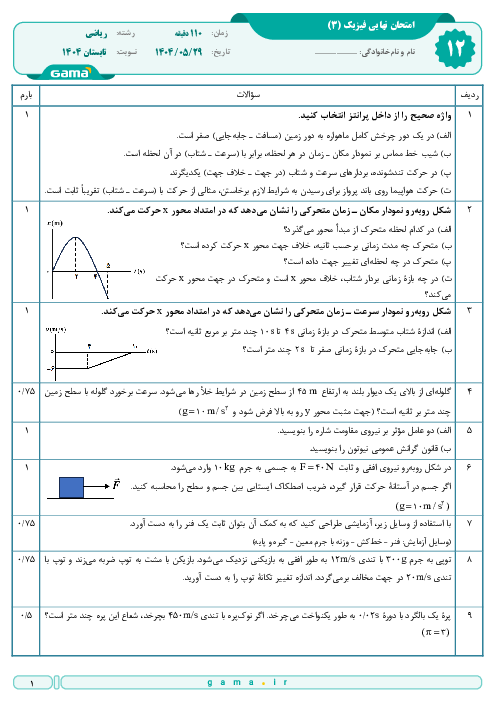
جسمی از حال سکون حرکت خود را با شتاب ثابت ${{a}_{1}}$ در یک مسیر مستقیم آغاز کرده و پس از $t$ ثانیه سرعت آن به $v$ میرسد. اگر جسم در ادامهٔ مسیر حرکت خود با شتاب ثابت ${{a}_{2}}$ حرکت کند و پس از $3t$ ثانیهٔ دیگر سرعت آن از $v$ به $-\frac{v}{2}$ برسد، تندی متوسط جسم در طول این حرکت چند $v$ است؟
تحلیل ویدئویی تست
سعید احمدوند 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...