مختصات نقطهٔ مینیمم نسبی تابع با ضابطهٔ کدام است؟ | حسابان (2) دوازدهم شماره 80118

گاما رو نصب کن!

درحال دریافت اطلاعات ...

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

قوانین و مقررات را خواندم و می پذیرم.

قبلا ثبت نام کرده اید؟ وارد شوید!

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد! )

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

ورود | ثبت نام

لطفا کمی صبر کنید ...

دوست خوبم!
برای نگهداری سابقه خریدتان، نیاز به شماره موبایل (یا ایمیل) شما داریم.

موبایل یا ایمیل

رمزعبور اگه یادت نیس نزن :)

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

منتظر دریافت پیامک شما ...

ورود با رمزعبور

برای استفاده بسیاری از امکانات گاما و خیلی از وبسایت ها باید جاوا اسکریپت را در مرورگر خود فعال کنید.

برای این کار باید به تنظیمات مرورگر خود مراجعه کنید.

جستجو

پربازدیدها: #{{ tag.title }}

نمونه سوال

فایل آموزشی

پرسش و پاسخ

آزمون آنلاین

درسنامه آموزشی

مدرسه یاب

جستجوهای پرتکرار

نمونه سوال

محتوای آموزشی

آزمون آنلاین

پرسش و پاسخ

درسنامه آموزشی

مدرسه یاب

معلم خصوصی

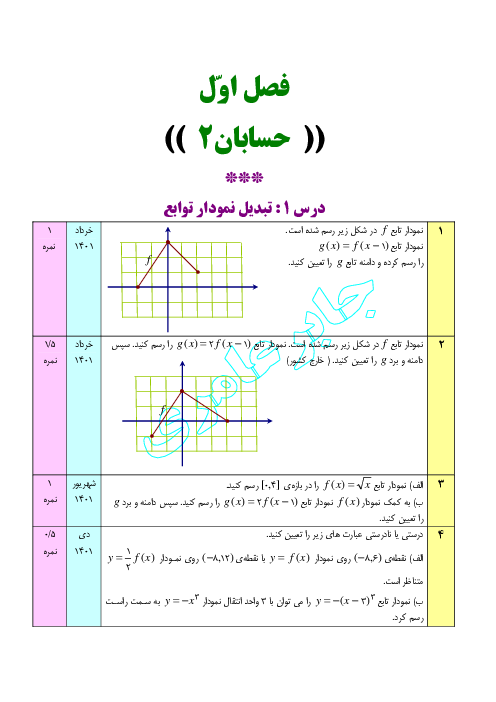
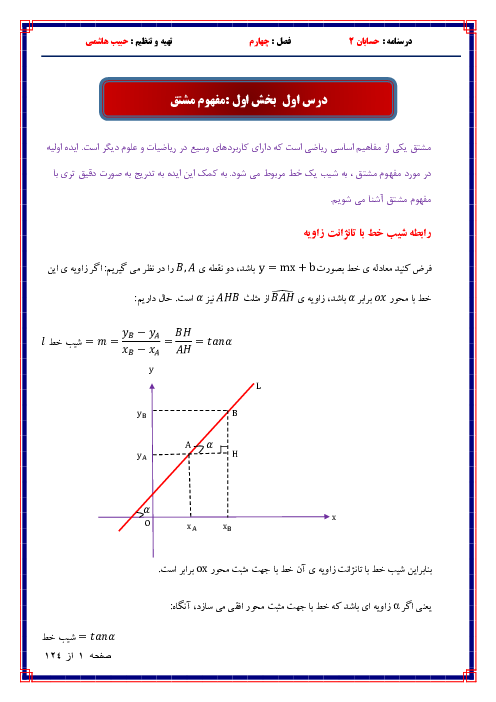
درس 1: اکسترمم‌های یک تابع و توابع صعودی و نزولی حسابان (2) دوازدهم دوره دوم متوسطه- نظری علوم ریاضی درسنامه آموزشی این مبحث

مختصات نقطهٔ مینیمم نسبی تابع با ضابطهٔ $y=\frac{4{{\ln }^{2}}x}{x}$ کدام است؟

1 )

$(1,0)$

2 )

$(e,\frac{4}{e})$

3 )

$(\frac{1}{e},-\frac{4}{e})$

4 )

$(-\frac{1}{e},-4e)$

نمایش پاسخ

$\begin{align}
& {y}'=\frac{(8\times \frac{1}{x}\ln x)x-4{{\ln }^{2}}x}{{{x}^{2}}}=0 \\
& \Rightarrow 8\ln x-4{{\ln }^{2}}x=0\Rightarrow 4\ln x(2-\ln x)=0 \\
& \Rightarrow \left\{ \begin{matrix}
\ln x=0\Rightarrow x=1\Rightarrow f(1)=0 \\
\ln x=2\Rightarrow x={{e}^{2}}\Rightarrow f({{e}^{2}})=\frac{16}{{{e}^{2}}} \gt 0 \\
\end{matrix} \right. \\
\end{align}$

نقطهٔ $(1,0)$ مینیمم است.

گزارش اشکال

یک تست دیگه بزن

یک آزمون کامل بده