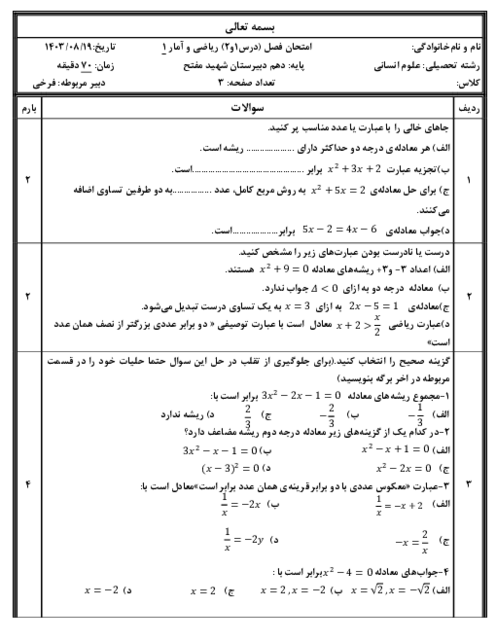
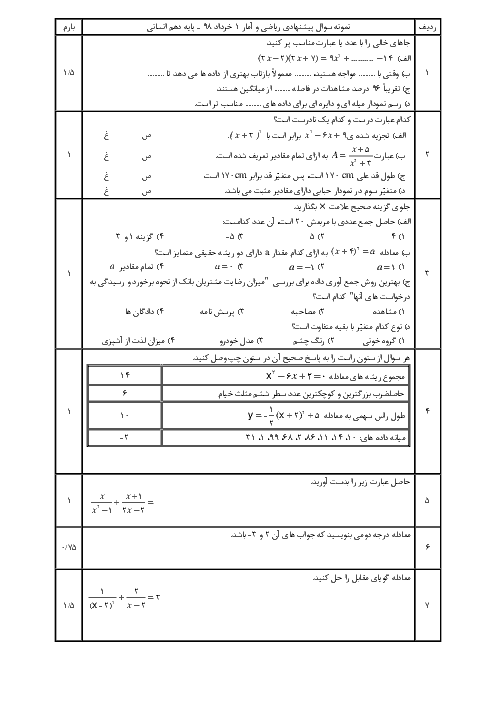
ابتدا هر دو معادله را حل می‌کنیم:

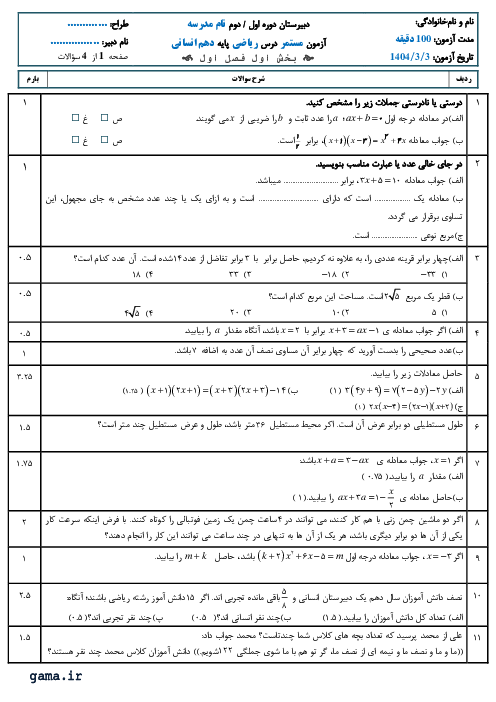
$\left( m+1 \right){{x}^{2}}+8x=0\to x\left[ \left( m+1 \right)x+8 \right]=0\to \left\{ \begin{matrix}
   x=0  \\
   \left( m+1 \right)x=-8\to x=\frac{-8}{m+1}  \\
\end{matrix} \right.$
$m{{x}^{2}}-18x=0\to x\left( mx-18 \right)=0\to \left\{ \begin{matrix}
   x=0  \\
   mx=18\to x=\frac{18}{m}  \\
\end{matrix} \right.$

منظور از ریشه‌ی مثبت یا منفی، ریشه‌ی غیر صفر معادلات مذکور است که طبق فرض سؤال داریم:

$\begin{align}
  & \frac{-8}{m+1}=\frac{18}{m}+10\xrightarrow{\div 2}\,\frac{-4}{m+1}=\frac{9}{m}+5\Rightarrow \frac{-4}{m+1}=\frac{9+5m}{m}\Rightarrow \left( m+1 \right)\left( 9+5m \right)=-4m \\ 
 & \Rightarrow 9m+9+5{{m}^{2}}+5m+4m=0\Rightarrow 5{{m}^{2}}+18m+9=0\to \left( m+3 \right)\left( 5m+3 \right)=0 \\ 
 & \Rightarrow \left\{ \begin{matrix}
   m+3=0\Rightarrow m=-3  \\
   5m+3=0\Rightarrow m=\frac{-3}{5}  \\
\end{matrix} \right. \\ 
\end{align}$

(چون به‌ازای این مقدار، $x=\frac{-8}{m+1}$ مقداری متفی خواهد شد.)

البته پس از تشکیل معادله‌ی $\frac{-8}{m+1}=\frac{18}{m}+10$ می‌توان اعداد موجود در گزینه‌ها را در این معادله امتحان نمود.