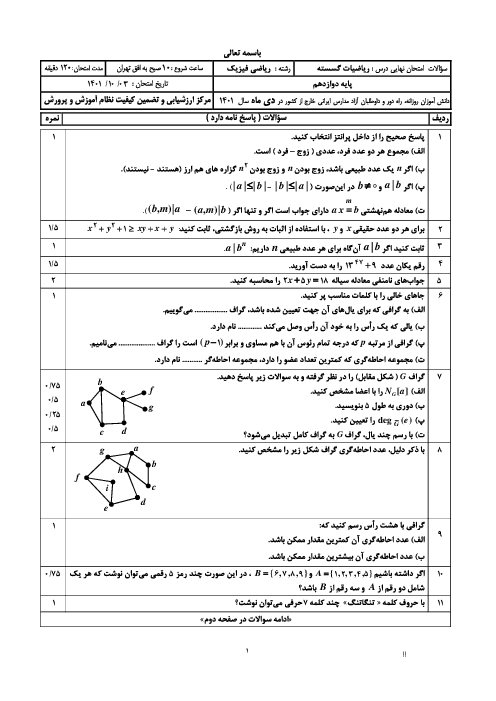
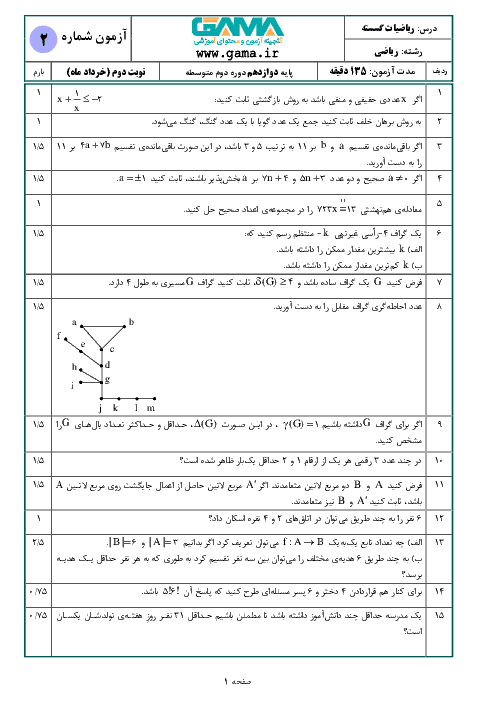
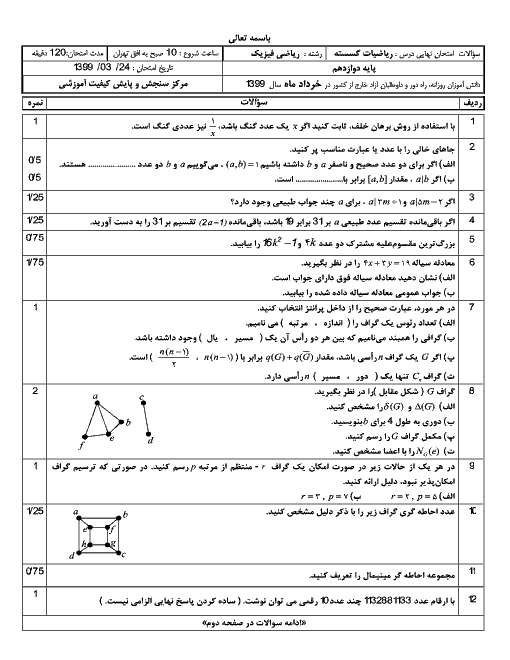
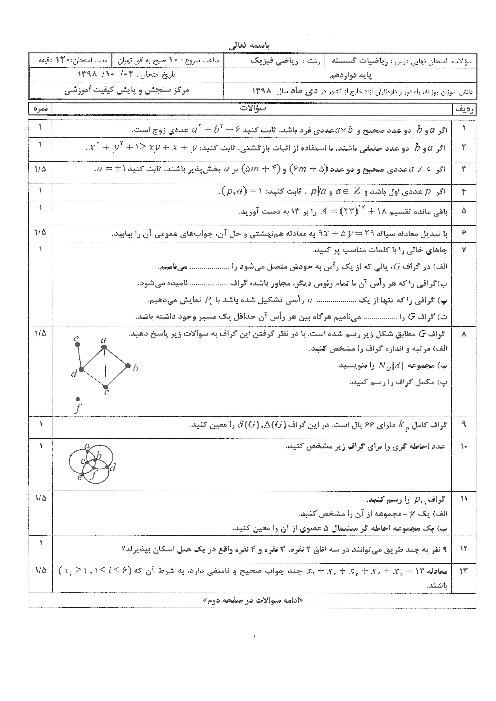
باقی‌ماندهٔ تقسیم توان‌های 11 بر 19 را به‌ترتیب حساب می‌کنیم:

${{11}^{1}}\overset{13}{\mathop{=}}\,11,\,\,\,\,\,\,\,\,\,\,{{11}^{2}}\overset{19}{\mathop{=}}\,121\overset{19}{\mathop{=}}\,121-6\times 19\overset{19}{\mathop{=}}\,7$

${{11}^{3}}\overset{19}{\mathop{=}}\,11\times 7\overset{19}{\mathop{=}}\,77\overset{19}{\mathop{=}}\,77-4\times 19\overset{19}{\mathop{=}}\,1$

اکنون اگر $n=3q+r$ که $0\le r\langle 3$، آن‌گاه

${{11}^{3}}\overset{19}{\mathop{=}}\,1\Rightarrow {{({{11}^{3}})}^{q}}\overset{19}{\mathop{=}}\,{{1}^{q}}\Rightarrow {{11}^{3q}}\overset{19}{\mathop{=}}\,1\Rightarrow {{11}^{3q}}\times {{11}^{r}}\overset{19}{\mathop{=}}\,{{11}^{r}}$

(با توجه به محاسبات بالا)

${{11}^{n}}={{11}^{3q+r}}\overset{19}{\mathop{=}}\,{{11}^{r}}\overset{19}{\mathop{=}}\,\left\{ \begin{matrix}   11\,\,\,\,r=1  \\   \begin{align}  & 7\,\,\,\,r=2 \\  & 1\,\,\,\,r=0 \\ \end{align}  \\\end{matrix} \right.$

در نتیجه ${{11}^{n}}\overset{19}{\mathop{=}}\,1$ اگر و فقط اگر باقی‌ماندهٔ تقسیم $n$ بر 3 برابر صفر باشد. پس برای یافتن پاسخ مسئله باید تعداد اعداد دو رقمی به‌صورت $3k$ را بیابیم.

$10\le 3k\le 99\Rightarrow 4\le k\le 33$

نتیجه می‌گیریم که $33-4+1=30$ عدد دو رقمی به‌صورت $3k$ وجود دارد.