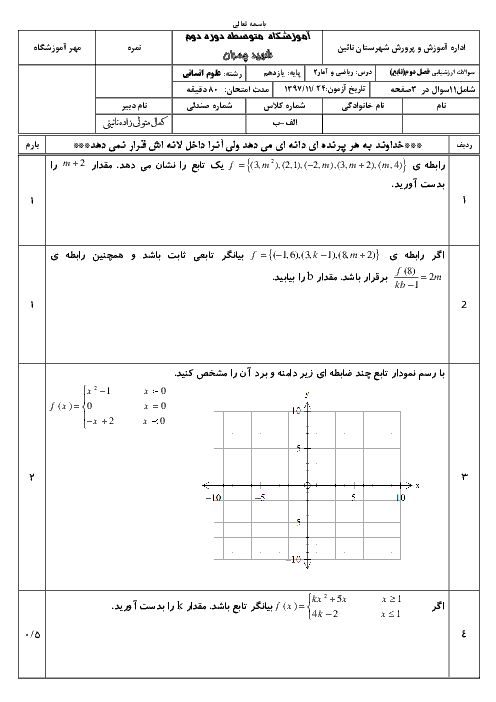
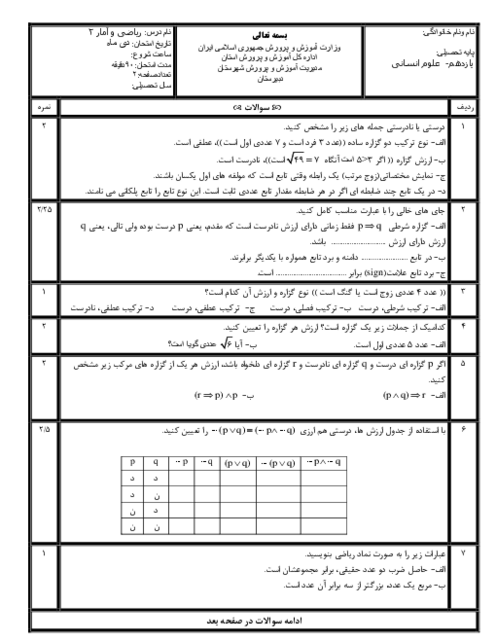
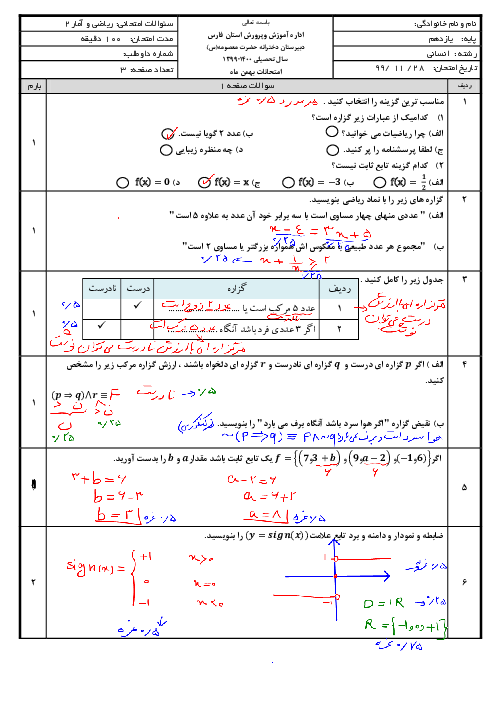
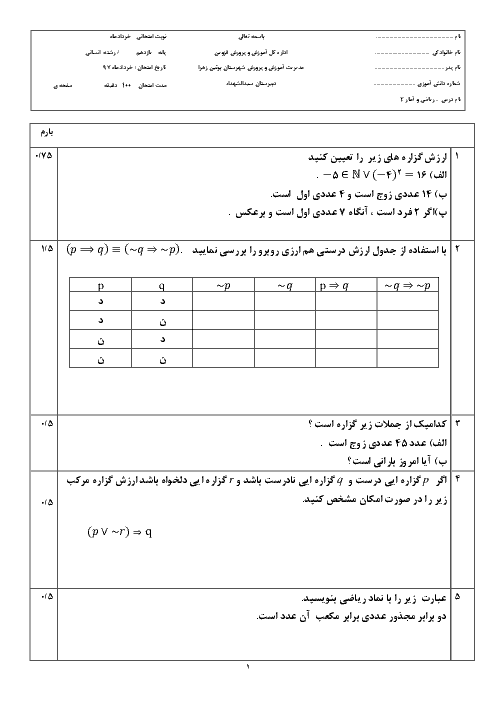
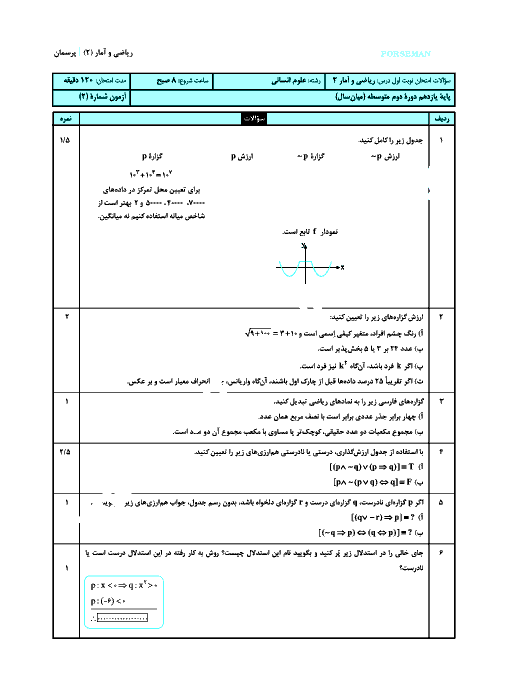
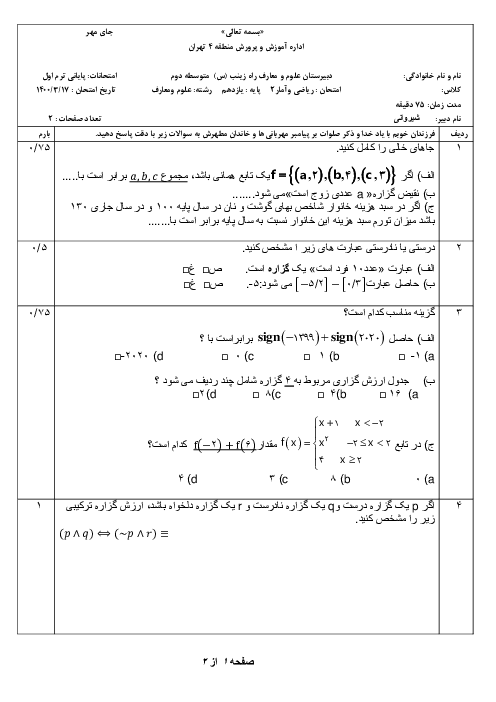
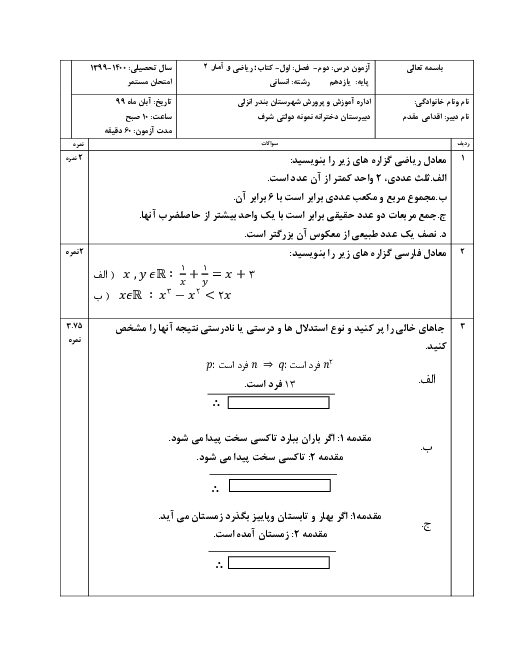
درس 1: توابع ثابت، چند ضابطه‌ای و همانی
ریاضی و آمار (2)
یازدهم
دوره دوم متوسطه- نظری
ادبیات و علوم انسانی
درسنامه آموزشی این مبحث
اگر $f=\left\{ (5,\sqrt{9}),(6,m-2n),(10,m+2n) \right\}$ تابعی ثابت و $g=\{(\frac{a}{2},1),(4,4),(8,b-2)\}$ تابعی همانی باشد، حاصل عبارت $m-n+a-b$ کدام است؟
تحلیل ویدئویی تست
عادل علی پناه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...