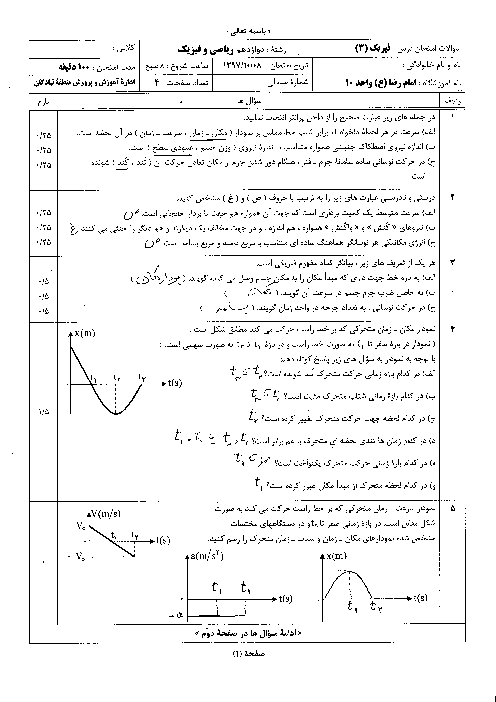
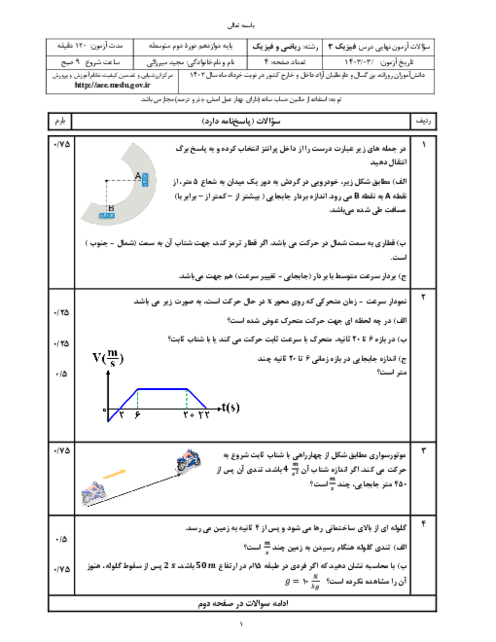
ابتدا با استفاده از معادله‌ی حرکت، ${{y}_{1}}$ و ${{y}_{2}}$ و سپس $\Delta x$ و $\Delta y$ را به دست می‌آوریم و سپس با استفاده از رابطه‌ی $\left| \Delta \overrightarrow{r} \right|=\sqrt{\Delta {{x}^{2}}+\Delta {{y}^{2}}}$، بزرگی تغییر مکان را حساب می‌کنیم.

$y=\frac{3}{4}x+1\Rightarrow \left\{ \begin{matrix} {{x}_{1}}=4m\Rightarrow {{y}_{1}}=\frac{3}{4}\times 4+1\Rightarrow {{y}_{1}}=4m  \\ {{x}_{2}}=12m\Rightarrow {{y}_{2}}=\frac{3}{4}\times 12+1\Rightarrow {{y}_{2}}=10m  \\ \end{matrix} \right.$

$\left\{ \begin{matrix} \Delta y={{y}_{2}}-{{y}_{1}}=10-4\Rightarrow \Delta y=6m  \\ \Delta x={{x}_{2}}-{{x}_{1}}=12-4\Rightarrow \Delta x=8m  \\ \end{matrix} \right.\xrightarrow{\left| \Delta \overrightarrow{r} \right|=\sqrt{\Delta {{x}^{2}}+\Delta {{y}^{2}}}}\left| \Delta \overrightarrow{r} \right|=\sqrt{64+36}=10m$

اکنون با استفاده از رابطه‌ی $\left| \overline{\overrightarrow{v}} \right|=\frac{\left| \Delta \overrightarrow{r} \right|}{\Delta t}$، بزرگی سرعت متوسط متحرک در بازه‌ی داده شده را حساب می‌کنیم:

$\left| {\bar{\vec{v}}} \right|=\frac{\left| \Delta \vec{r} \right|}{\Delta t}\xrightarrow[\left| \Delta \vec{r} \right|=10m]{\Delta t=7-2=5s}\left| {\bar{\vec{v}}} \right|=\frac{10}{5}\Rightarrow \left| {\bar{\vec{v}}} \right|=2\frac{m}{s}$