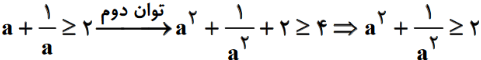کدام یک از عبارت‌های زیر، یک قضیهٔ دو شرطی است؟ $\left( a,k\in \mathbb{R} \right)$
1 )
اگر $a+\frac{1}{2}\ge 2$ باشد، آنگاه ${{a}^{2}}+\frac{1}{{{a}^{2}}}\ge 2$ است.
2 )
اگر $a \gt 0$ باشد، آنگاه $a\ne -1$ است.
3 )
اگر $\alpha $ و $\beta $ گنگ باشد، آنگاه $\alpha -\beta $ گنگ است.
اگر ${{k}^{3}} \gt {{k}^{2}}$ باشد، آنگاه $k \gt 1$ است.
پاسخ تشریحی :
تحلیل ویدئویی تست
محسن ذوالفقاری 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...