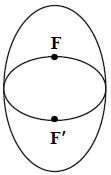
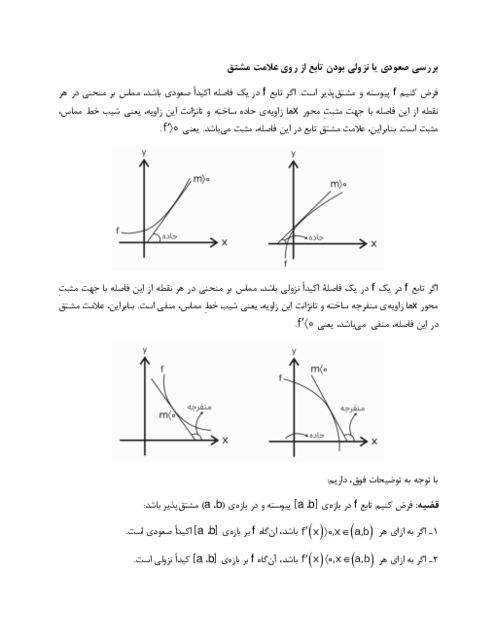
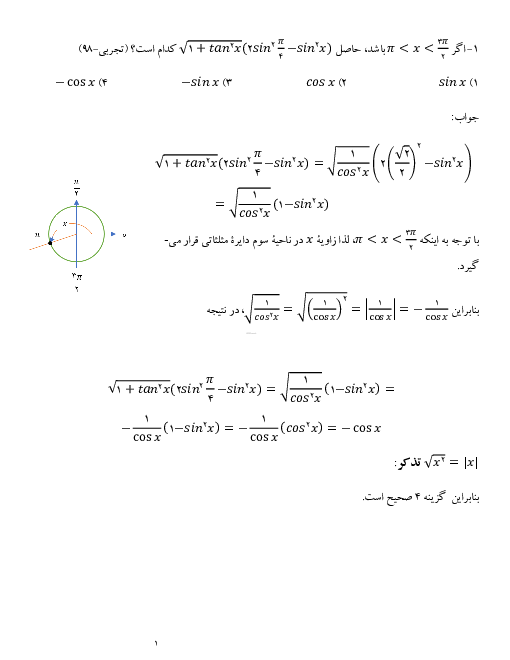
پارامترهای بيضی بزرگ‌تر را با $a$، $b$و $c$ و بيضی كوچك‌تر را با ${a}'$، ${b}'$ و ${c}'$ نمایش می‌دهیم.

طول قطر بزرگ بيضی افقی با طول قطر كوچك بيضی قائم مساوی است، پس: ${a}'=b$. همچنين فاصله‌ی كانونی بيضی قائم برابر طول قطر كوچك بيضی افقی است، پس: ${b}'=c$ 

خروج از مركز بيضی قائم برابر $\frac{3}{5}$ است، پس: $e=\frac{c}{a}=\frac{3}{5}\Rightarrow a=\frac{5c}{3}$ 

خروج از مركز بيضی افقی برابر است با:

${e}'=\frac{{{c}'}}{{{a}'}}=\sqrt{\frac{{{({c}')}^{2}}}{{{({a}')}^{2}}}}=\sqrt{\frac{{{({a}')}^{2}}-{{({b}')}^{2}}}{{{({a}')}^{2}}}}=\sqrt{\frac{{{b}^{2}}-{{c}^{2}}}{{{b}^{2}}}}=\sqrt{\frac{({{a}^{2}}-{{c}^{2}})-{{c}^{2}}}{{{a}^{2}}-{{c}^{2}}}}=\sqrt{\frac{{{a}^{2}}-2{{c}^{2}}}{{{a}^{2}}-{{c}^{2}}}}=\sqrt{\frac{\frac{25}{9}{{c}^{2}}-2{{c}^{2}}}{\frac{25}{9}{{c}^{2}}-{{c}^{2}}}}\sqrt{\frac{\frac{25}{9}-2}{\frac{25}{9}-1}}=\sqrt{\frac{7}{16}}=\frac{\sqrt{7}}{4}$