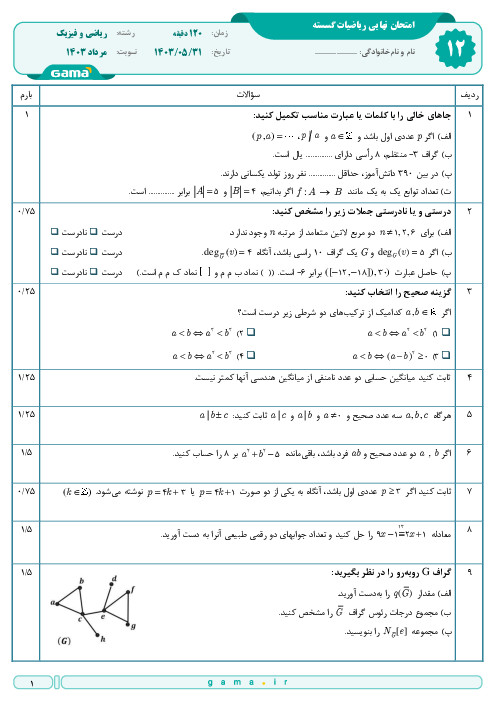
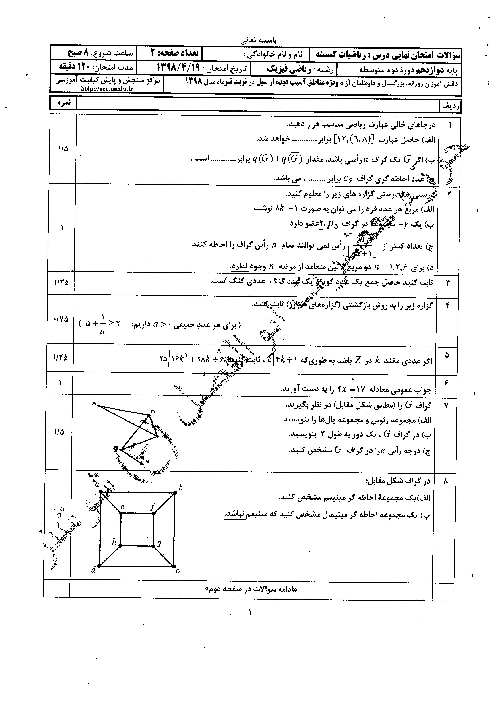
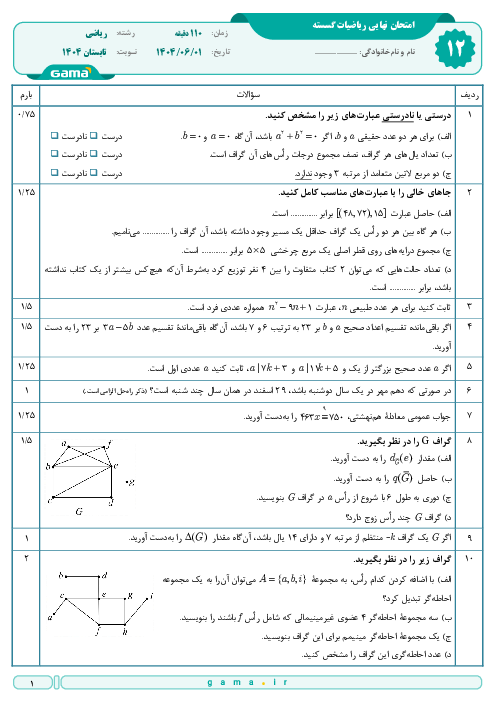
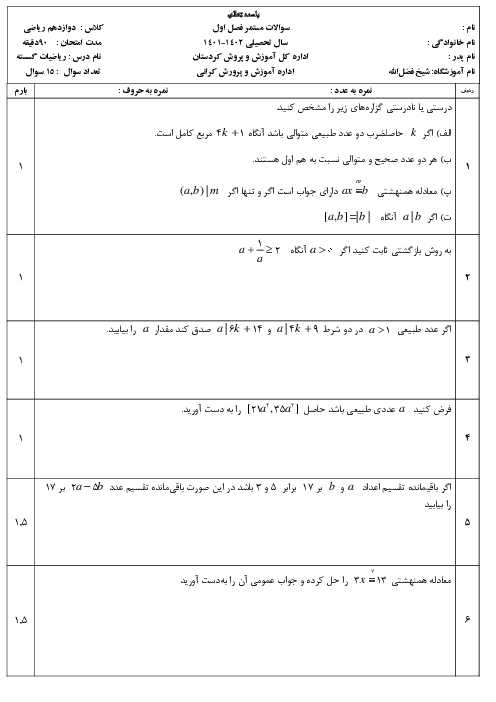
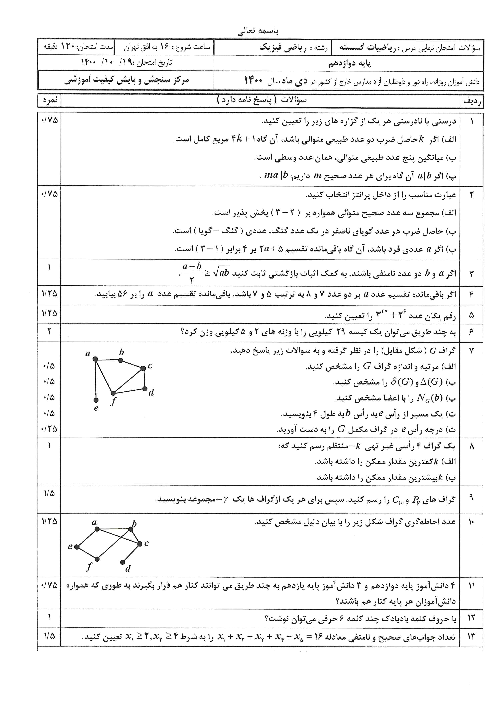
درس 2: بخش‌پذیری در اعداد صحیح
ریاضیات گسسته
دوازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
برای هر سه عدد حقیقی x, y, z ثابت کنید: ${x^2} + {y^2} + {z^2} \geqslant xy + yz + xz$
پاسخ تشریحی :
تحلیل ویدئویی تست
امیرحسین ذولفی 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...