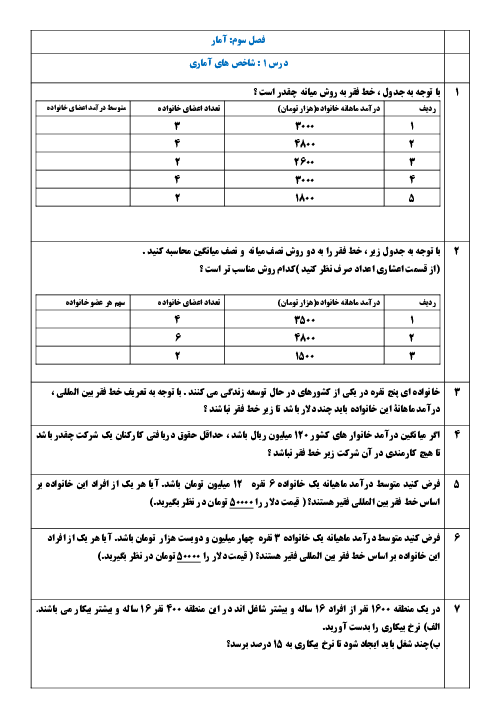
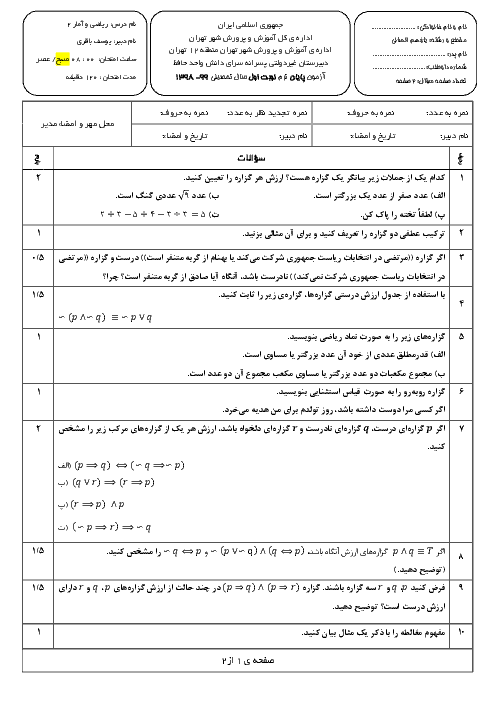
درس 1: توابع ثابت، چند ضابطهای و همانی
ریاضی و آمار (2)
یازدهم
متوسطه دوم نظری
ادبیات و علوم انسانی
درسنامه آموزشی این مبحث
زوج مرتب $(1,{{n}^{2}}+n-1)$ روی نيمساز ناحيۀ اول و سوم قرار دارد. مجموع مقادير ممكن $n$ كدام است؟