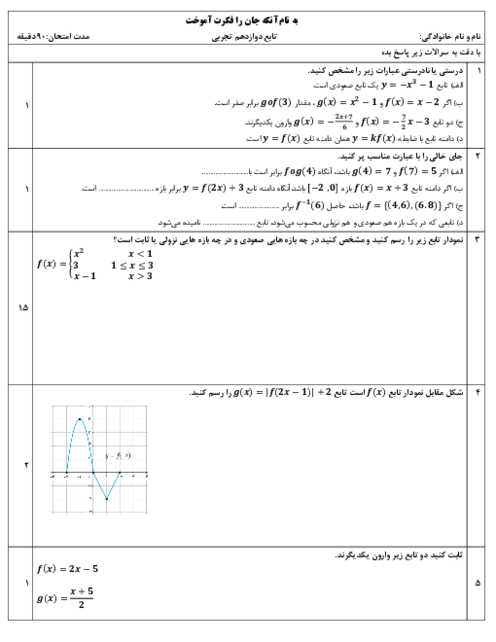
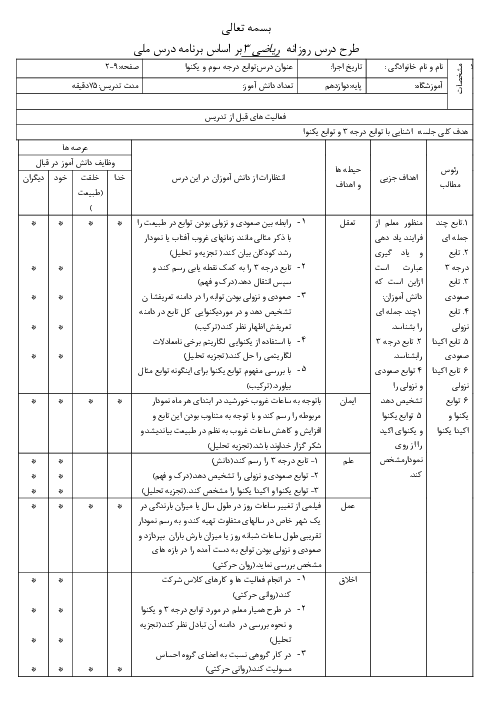
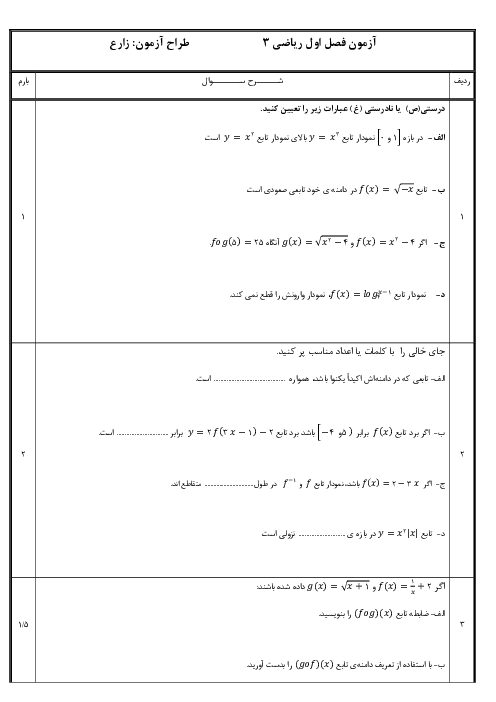
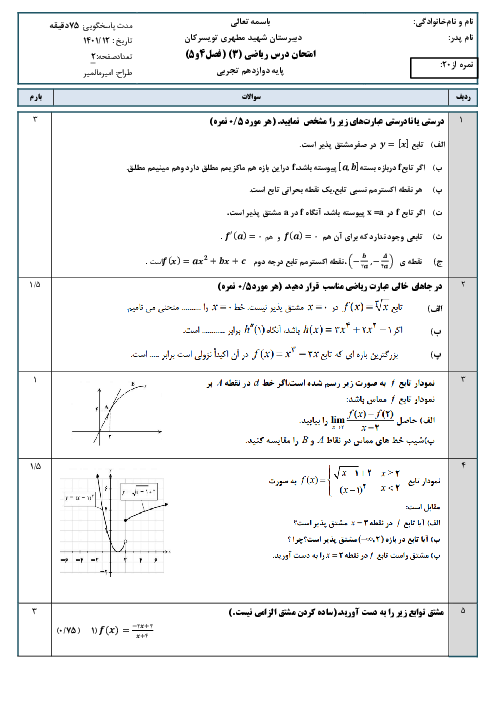
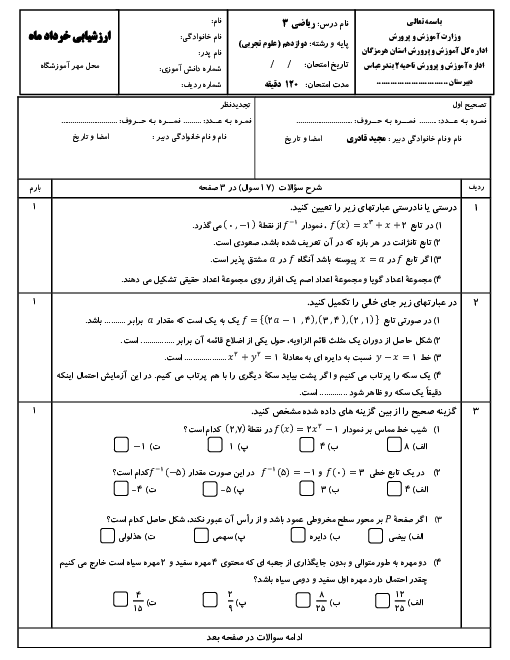
نكته: اگر صورت يا مخرج تابع $\frac{f(x)}{g(x)}$ شامل عبارت راديكالی باشد و $\underset{x\to a}{\mathop{\lim }}\,f(x)=\underset{x\to a}{\mathop{\lim }}\,g(x)=0$، آنگاه برای محاسبه‌ی $\underset{x\to a}{\mathop{\lim }}\,\frac{f(x)}{g(x)}$، ابتدا صورت و مخرج را در عبارت راديكالی مناسب ضرب می‌كنيم تا عامل $(x-a)$ يا عاملی كه موجب صفر شدن حد $f(x)$ و $g(x)$ در این نقطه شده است، ظاهر شود. سپس با ساده كردن آن از صورت و مخرج، حاصل حد را محاسبه می‌كنيم.

نکته ${{a}^{3}}+{{b}^{3}}=(a+b)({{a}^{2}}-ab+{{b}^{2}})$ 

با استفاده از نكات بالا داريم:

\[\underset{x\to -2}{\mathop{\lim }}\,\frac{\sqrt{x+3}-1}{\sqrt[3]{4x}+2}\times \frac{\sqrt{x+3}+1}{\sqrt{x+3}+1}\times \frac{\sqrt[3]{16{{x}^{2}}}-2\sqrt[3]{4x}+4}{\sqrt[3]{16{{x}^{2}}}-2\sqrt[3]{4x}+4}=\underset{x\to -2}{\mathop{\lim }}\,\frac{(x+3-1)(\sqrt[3]{16{{x}^{2}}}-2\sqrt[3]{4x}+4)}{(4x+8)(\sqrt{x+3}+1)}=\underset{x\to -2}{\mathop{\lim }}\,\frac{(x+2)(\sqrt[3]{16{{x}^{2}}}-2\sqrt[3]{4x}+4)}{4(x+2)(\sqrt{x+3}+1)}=\frac{4+4+4}{4(1+1)}=\frac{12}{8}=\frac{3}{2}=1/5\]