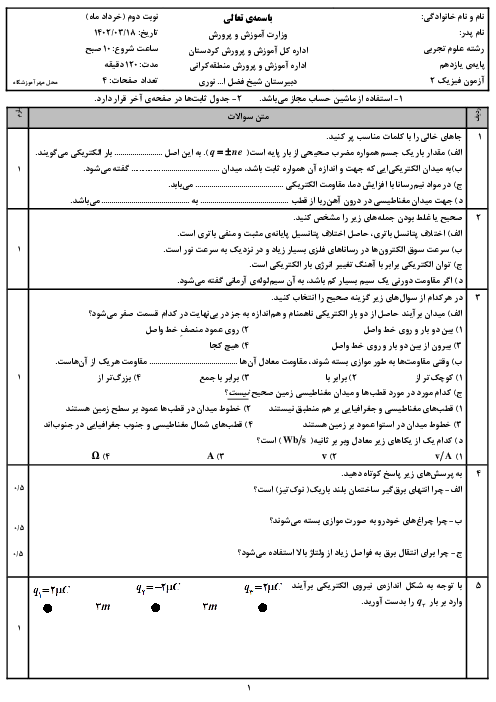
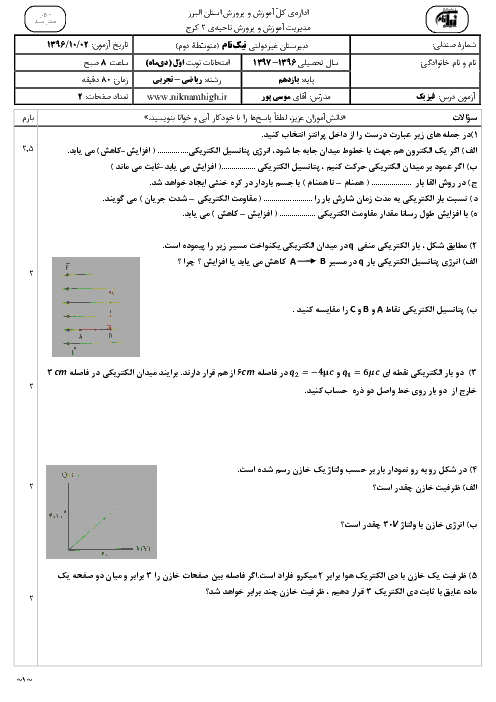
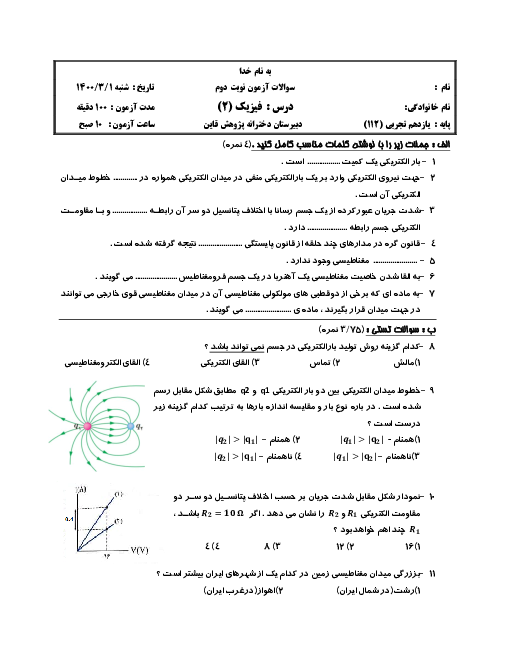
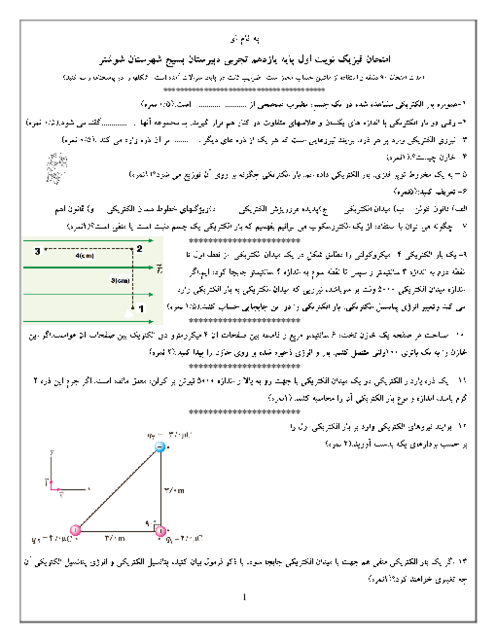
یک ذره به جرم 8 در 10 به توان منفی 27 و بار الکتریکی 1.6 در ده به توان منفی 13 میکروکولن در یک میدان الکتریکی یکنواخت به بزرگی 10 به توان 3 نیوتون بر کولن از حال سکون رها میشود ، اگر تنها نیروی وارد بر ذره از طرف این میدان باشد ، تندی این ذره پس از چند سانتی متر جا به جایی به 10 به توان 5 متر بر ثانیه خواهد رسید ؟ 1) 2.5 2) 25 3) 5 4) 50 لطفا راه حل را هم وارد کنید .
تندی این ذره پس از چند سانتی متر جا به جایی به 10 به توان 5 متر بر ثانیه خواهد رسید ؟
پاسخ ها: {{ repliesNum }}
پاسخ انتخاب شده
در پاسخ به: {{ reply.reply_to.name }}
در پاسخ به
این پیام حذف شده است.