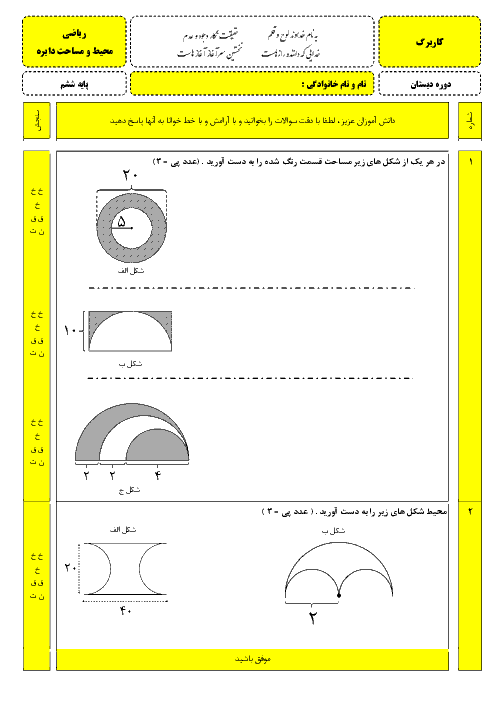
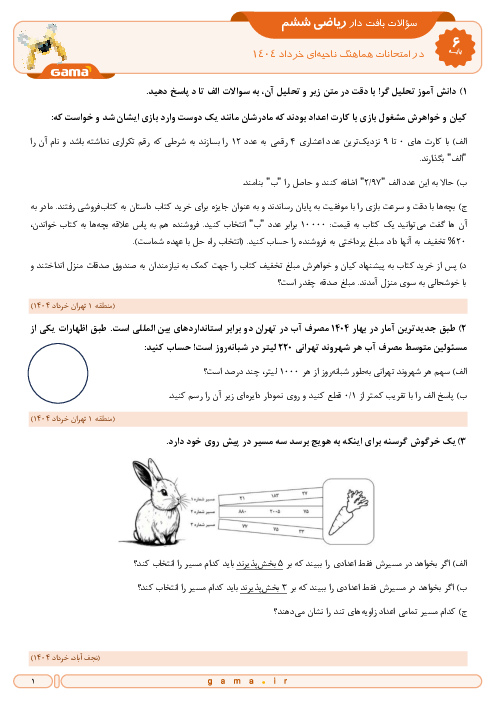
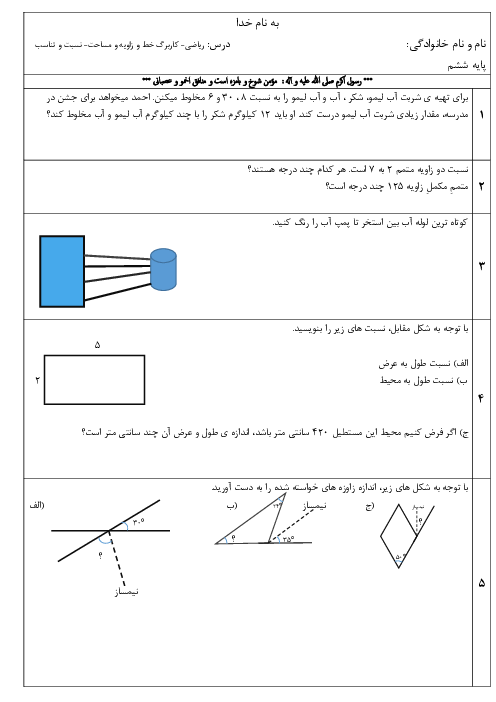
کسر های تلسکوپی چیستند و ضرب و تقسیم و جمع و تفریق آنها چگونه است
جدیدترین پاسخها
بهترین پاسخها
![]()
پاسخ ها: {{ repliesNum }}
پاسخ انتخاب شده
در پاسخ به: {{ reply.reply_to.name }}
در پاسخ به
این پیام حذف شده است.