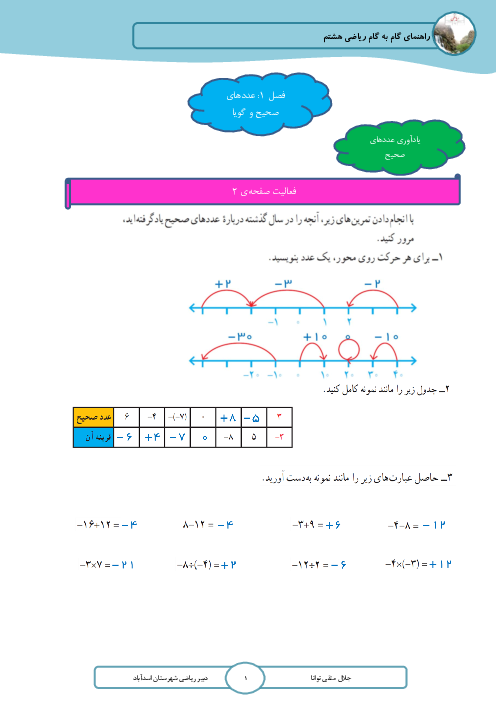
با رسم سه مماس بر دایره ی O ، مثلث PAB تشکیل می شود. اگر 40=APB ، آن گاه زاویه AOB برابر است با: الف) ۴۵⁰ ب)50⁰ ج)55⁰ د)70⁰
با رسم سه مماس بر دایرهی O ، مثلث PAB تشکیل می شود. اگر 40=APB ، آن گاه زاویه AOB برابر است با:
پاسخ ها: {{ repliesNum }}
پاسخ انتخاب شده
در پاسخ به: {{ reply.reply_to.name }}
در پاسخ به
این پیام حذف شده است.