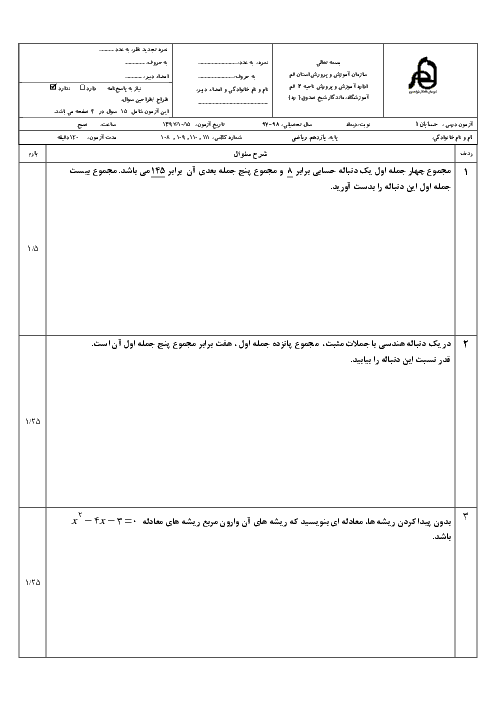
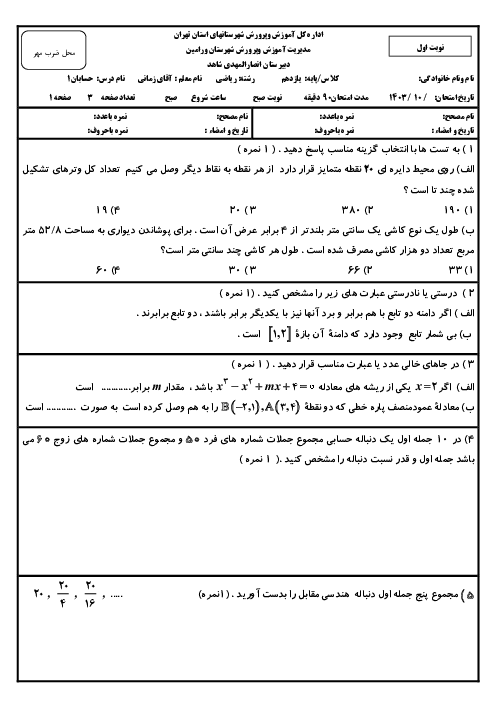
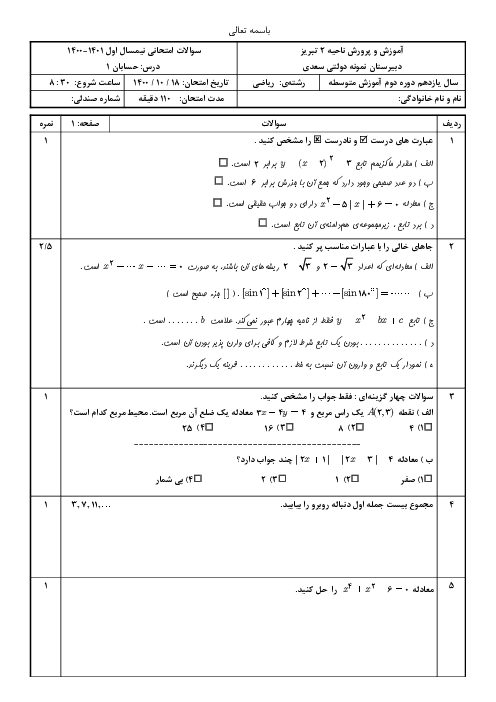
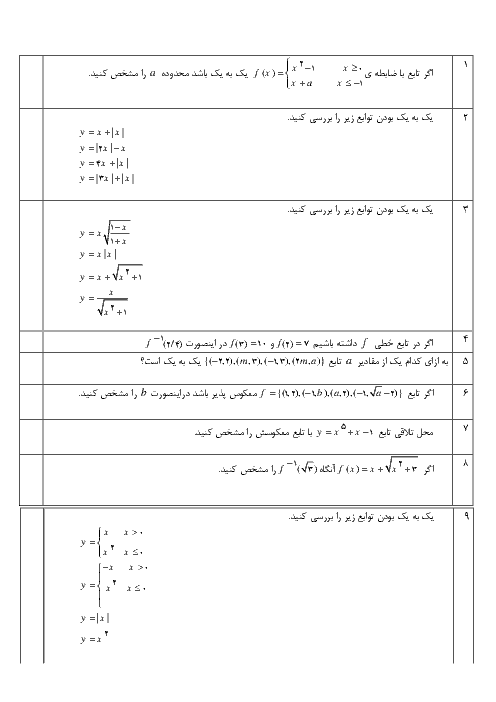
میگه اگر s اندیس 1 تا 3 مجموع n جمله ی اول سه تا دنباله حسابی با جمله اول 1 ، و به ترتیب قدر نسبت 1 تا 3 باشن ثابت کن اینا خودشون دنباله حسابی ان. راه حلشم چنین چیزی داده ولی متوجه نمیشم میشه یکی توضیح بده ؟ S_{1(n+1)} - S_{1n} = \frac{(n+1)(n+2)}{2} - \frac{n(n+1)}{2} = \frac{(n+1)(n+2-n)}{2} = \frac{2(n+1)}{2} = n+1 S_{2(n+1)} - S_{2n} = (n+1)^{2} - n^{2} = n^{2} + 2n + 1 - n^{2} = 2n + 1 S_{3(n+1)} - S_{3n} = \frac{(n+1)(3n+2)}{2} - \frac{n(3n-1)}{2} = \frac{3n^{2} + 5n + 2 - 3n^{2} + n}{2} = \frac{6n + 2}{2} = 3n + 1
مجموع دنبالههای حسابی در حسابان یازدهم
پاسخ ها: {{ repliesNum }}
پاسخ انتخاب شده
در پاسخ به: {{ reply.reply_to.name }}
در پاسخ به
این پیام حذف شده است.