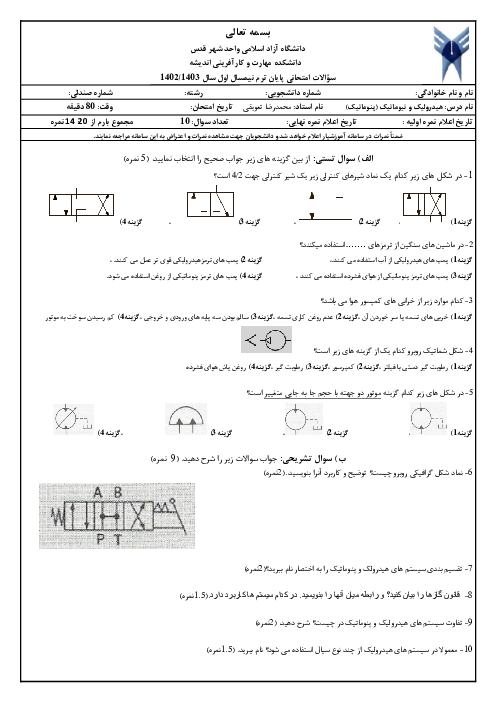
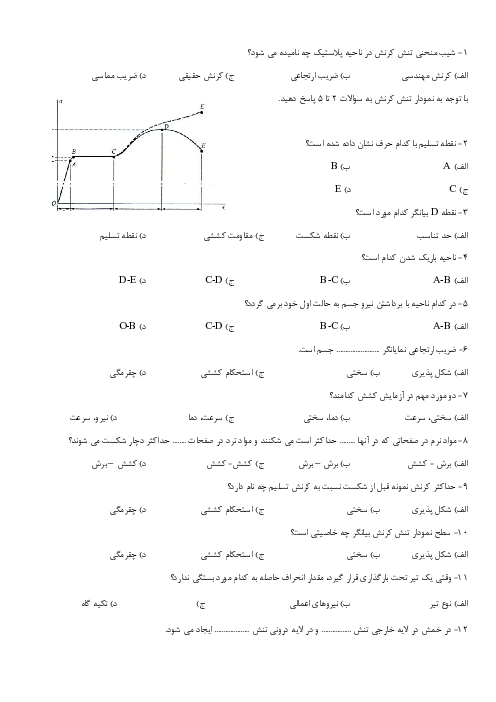
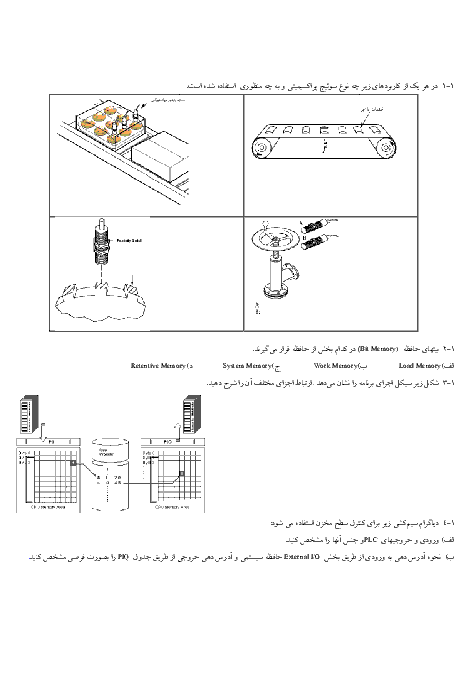
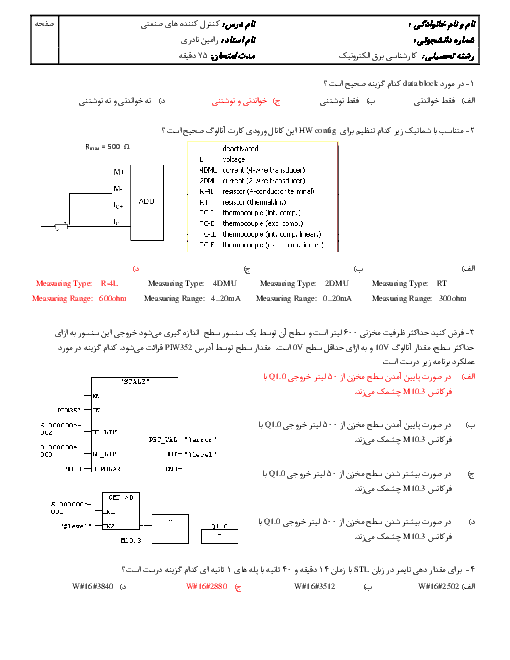
آرژین راشت این هم یک سوال ترکیبیِ فوقحرفهای از ریاضی و فیزیک که ذهن دانشمندان رو هم به چالش میکشه: --- ### مسئلهٔ پیشرفته: “پارادوکس سیاهچالهٔ کوانتومی“ یک سیاهچالهٔ شوارتزشیلد با جرم \( M \) داریم. افق رویداد آن در شعاع \( r_s = \frac{2GM}{c^2} \) قرار دارد. حالا فرض کنید یک ذرهٔ کوانتومی با جرم \( m \ll M \) در فاصلهٔ \( r = r_s + \delta \) (که \( \delta \to 0^+ \)) قرار دارد. #### الف) محاسبهٔ ریاضی (نسبیت عام): با استفاده از متریک شوارتزشیلد، نشان دهید زمانِ سقوط ذره به داخل سیاهچاله (\( \tau \)) از دید ناظرِ دوردست، بینهایت است: $ t \approx \frac{r_s}{c} \ln \left( \frac{r_s}{\delta} \right) \quad \text{هنگام} \quad \delta \to 0^+ $ #### ب) تناقض کوانتومی: در مکانیک کوانتومی، ذره دارای طول موج کامپتون (\( \lambda_c = \frac{h}{mc} \)) است. اگر \( \delta < \lambda_c \) باشد: - چرا این حالت با اصل عدم قطعیت هایزنبرگ تناقض دارد؟ - آیا تابش هاوکینگ میتواند این تناقض را حل کند؟ (توضیح کوتاه دهید.) #### ج) محاسبهٔ حدی: اگر \( M = 10 \, \text{M}_\odot \) (جرم خورشیدی) و \( m = m_p \) (جرم پروتون) باشد: 1. \( r_s \) و \( \lambda_c \) را محاسبه کنید. 2. شرط \( \delta < \lambda_c \) را بررسی کنید. آیا این شرط در جهان واقعی امکانپذیر است؟ --- ### راهنمایی برای حل: - برای (الف): از معادلهٔ ژئودزیک در متریک شوارتزشیلد استفاده کنید. - برای (ب): اصل عدم قطعیت: \( \Delta x \Delta p \geq \frac{\hbar}{2} \). - برای (ج): - \( \text{M}_\odot = 2 \times 10^{30} \, \text{kg} \), \( m_p = 1.67 \times 10^{-27} \, \text{kg} \), \( G = 6.67 \times 10^{-11} \), \( c = 3 \times 10^8 \), \( h = 6.63 \times 10^{-34} \). --- ### پاسخهای کوتاه (اگر گیر کردی!): <details> <summary>🔎 <strong>کلیک کن تا راهنمایی ببینید</strong></summary> - الف): $ \frac{dt}{dr} = -\frac{1}{c} \left(1 - \frac{r_s}{r}\right)^{-1} \implies t \sim \int \frac{dr}{1 - r_s/r} \quad \text{(انتگرالگیری)}. $ - ب): اگر \( \delta < \lambda_c \)، مکان ذره آنقدر دقیق میشود که انرژی آن (طبق اصل عدم قطعیت) به \( \infty \) میل میکند! تابش هاوکینگ با ایجاد جفت ذرهمجازی این تناقض را حل میکند. - ج): $ r_s \approx 30 \, \text{km}, \quad \lambda_c \approx 10^{-15} \, \text{m} \implies \delta < 10^{-15} \, \text{m} \quad \t آ.ر: *“اینجوری بگم: اگه این مسئله رو حل کنی، استیون هاوکینگ از بهشت برات دست میزنه!“*
پارادوکس سیاهچاله کوانتومی در فنی و مهندسی
پاسخ ها: {{ repliesNum }}
پاسخ انتخاب شده
در پاسخ به: {{ reply.reply_to.name }}
در پاسخ به
این پیام حذف شده است.