چالش‌های پیشرفته در تابع کولاتز برای دهم ریاضی

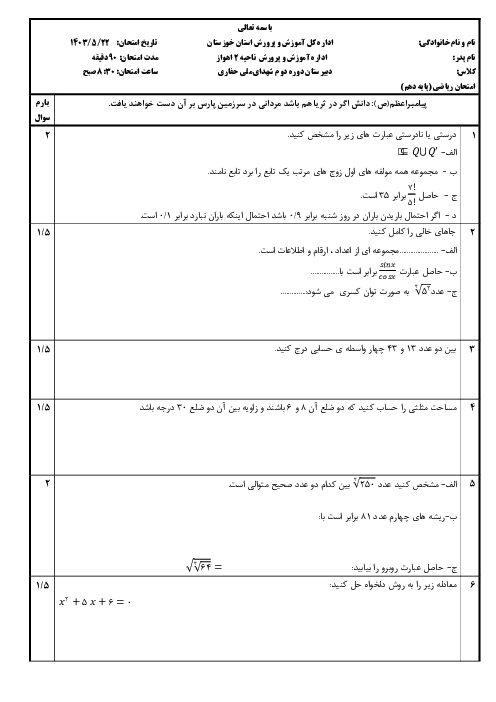
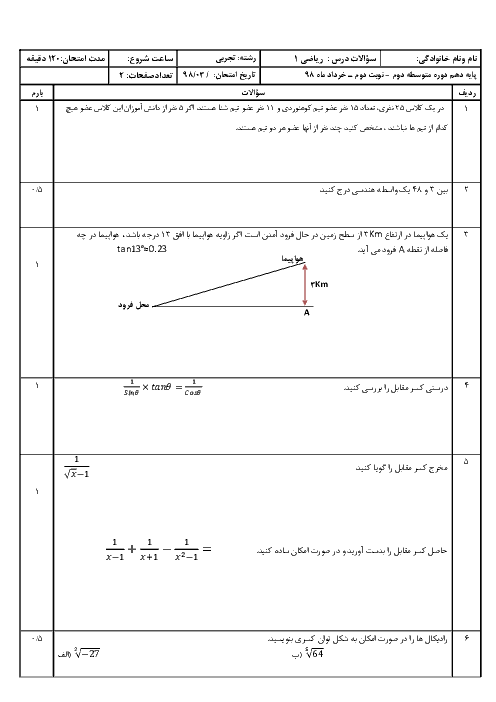
آ.ر:این سوال جزو سخت ترین سوال هاست که من این رو از استادم گرفتم. این هم یک سوال ریاضیِ چالشی ترکیبی از حسابان و نظریه اعداد که حتی ریاضیدان‌ها رو به فکر فرو می‌بره: ### مسئلهٔ پیشرفته: فرض کنید تابع \( f: \mathbb{N} \to \mathbb{N} \) به صورت زیر تعریف شده است: $ f(n) = \begin{cases} \frac{n}{2} & \text{if } n \text{ زوج باشد}, \\ 3n + 1 & \text{if } n \text{ فرد باشد}. \end{cases} $ حدس کولاتز ادعا می‌کند که برای هر عدد طبیعی \( n \)، دنباله‌ی \( f(n), f(f(n)), \ldots \) نهایتاً به 1 می‌رسد. الف) ثابت کنید یا رد کنید که برای هر \( n \equiv 4 \pmod{6} \)، این دنباله حتماً به 1 می‌رسد. ب) اگر \( n = 2^k - 1 \) (برای \( k \geq 2 \))، رفتار دنباله را برای \( k = 3, 4, 5 \) تحلیل کنید. --- ### راهنمایی برای حل: - برای قسمت الف: از استقرا یا بررسی همارزی‌های مدولاری استفاده کنید. - برای قسمت ب: دنباله را برای \( n = 7, 15, 31 \) محاسبه و الگوها را استخراج کنید. آ.ر“این مسئله آنقدر سخته که حتی کامپیوترها هم برای \( n \)های بزرگ کم میارن.