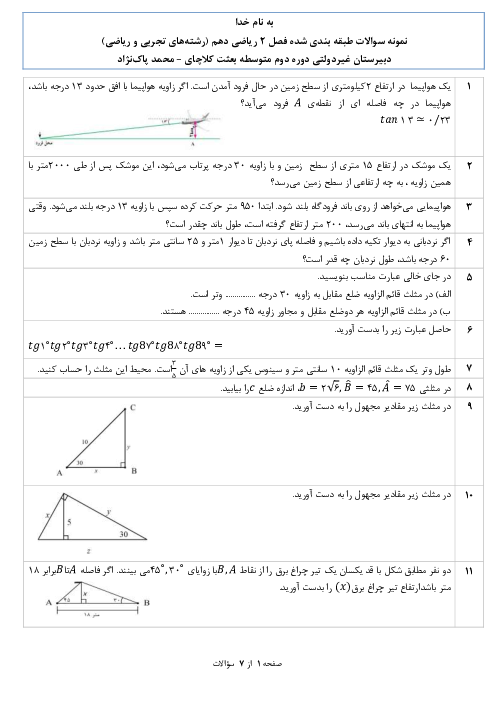
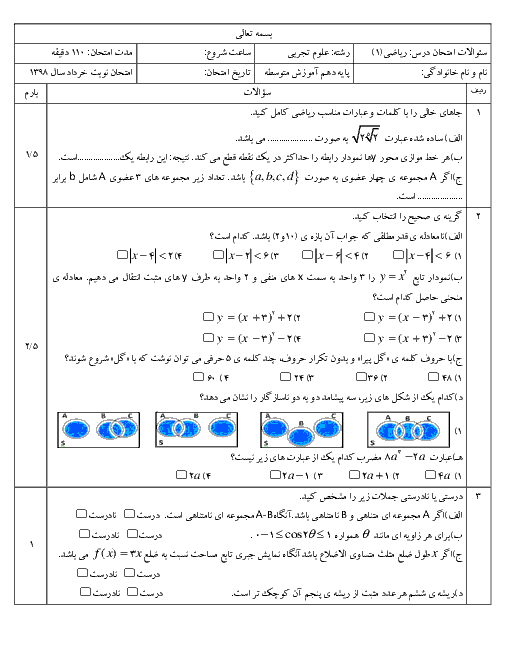
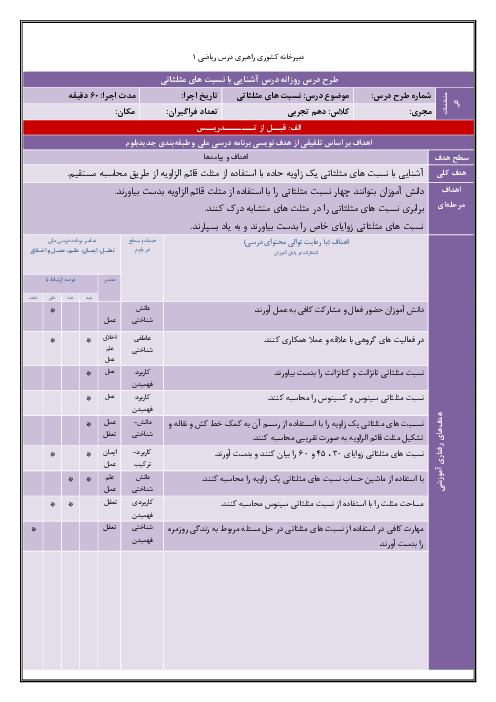
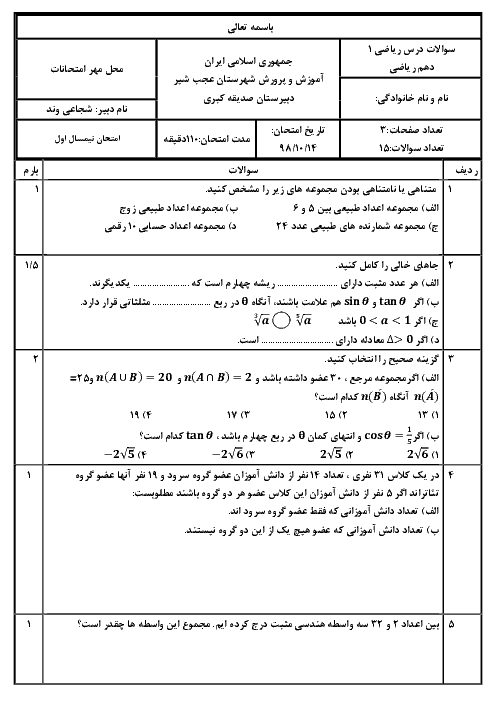
سلام چطور میتونیم از روی برد دامنه رو بدست آورد. اگر برد تابع خطی. fx=-x+2. به صورت [3وR=(0 باشد دامنه را بدست آورید .
بدست آوردن دامنه تابع خطی با شرایط خاص
پاسخ ها: {{ repliesNum }}
پاسخ انتخاب شده
در پاسخ به: {{ reply.reply_to.name }}
در پاسخ به
این پیام حذف شده است.