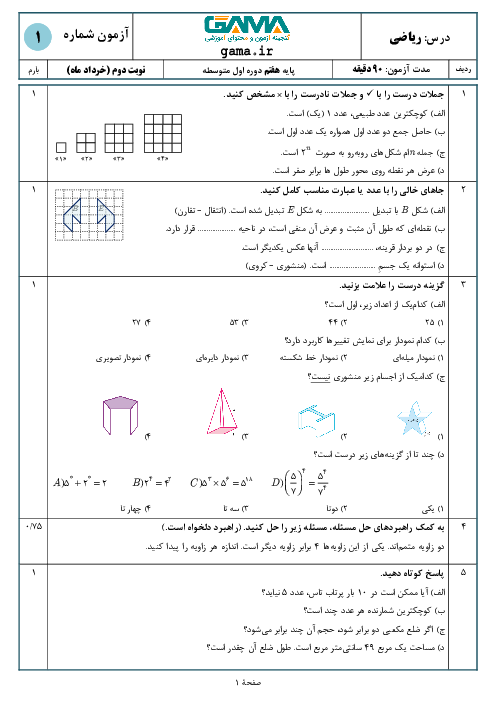
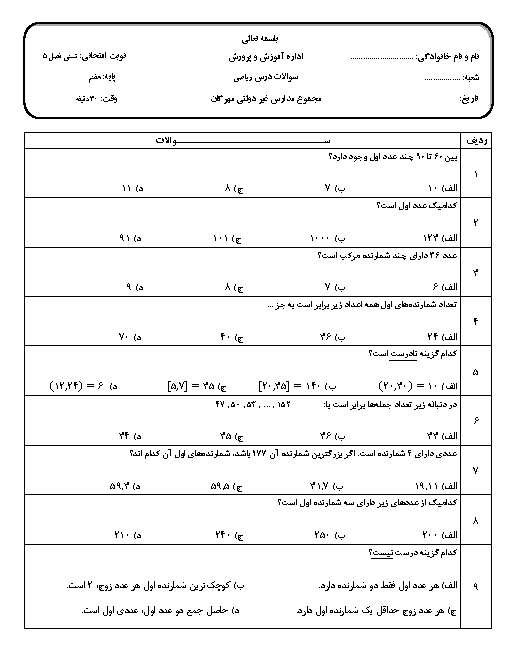
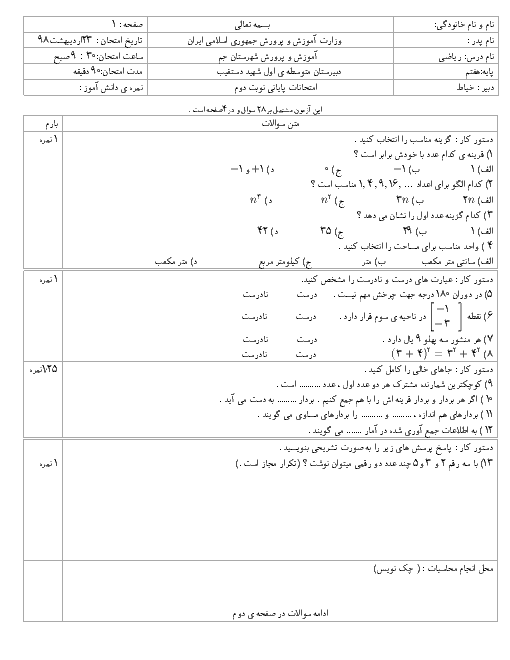
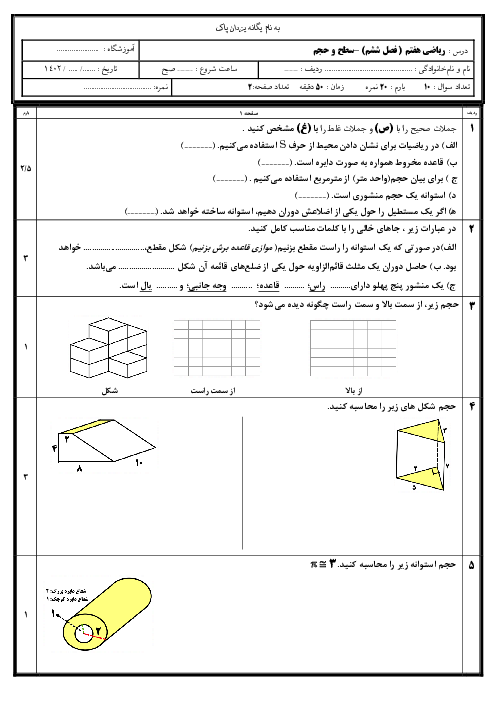
چند مثلث می توان برش داد که هر ضلع آن دارای طول طبیعی ( برحسب سانتی متر ) و دارای محیط 15 باشد ؟؟
تعداد مثلثهای با محیط 15 و ضلعهای طبیعی در ریاضی هفتم
پاسخ ها: {{ repliesNum }}
پاسخ انتخاب شده
در پاسخ به: {{ reply.reply_to.name }}
در پاسخ به
این پیام حذف شده است.