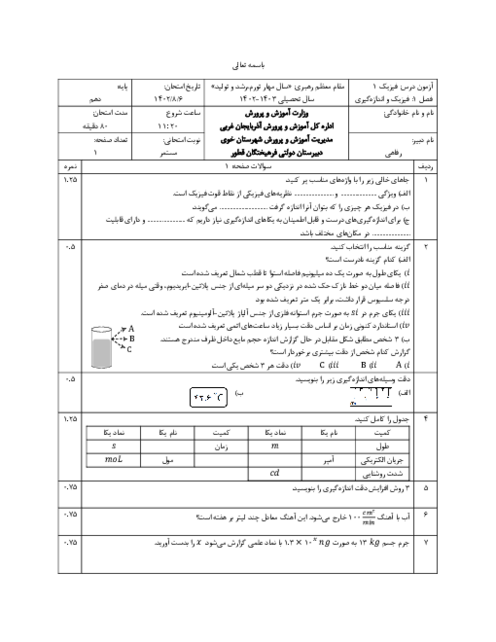
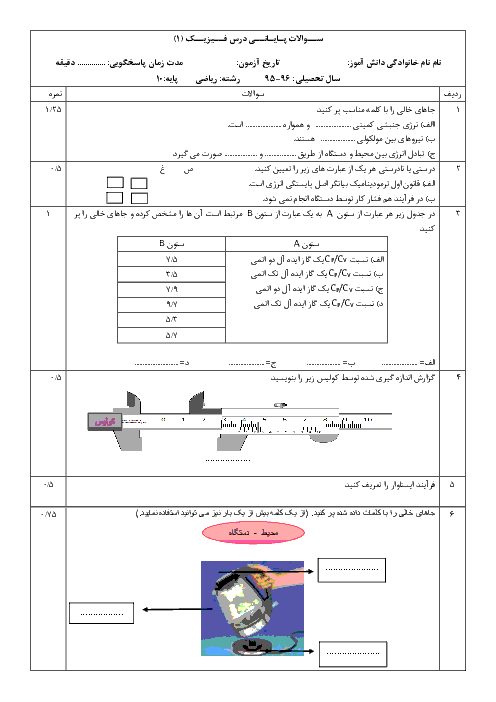
یه سوال داشتم... اگر به یک جسم از جهات مختلف نیرو وارد شود، چطور میتوانیم نیروی برآیند آن را بدست بیاوریم؟ مثلا یه نیرو با زاویه 37 درجه نسبت به افق و دیگری مخالف آن نیرو به زاویه ای مساوی با افق و نیرویی عمود. بر جسم و نیروی وزن این نیرو ها رو به من داده، من باید چجوری برآیند شون رو بدست بیارم؟ نیروی برایند و اینکه یه سوال دیگا هم داشتم آیا فرقی بین جمع جبری کار نیرو ها و کار برآیند نیرو ها وجود دارد؟ ممنون میشم پاسخ بدین🌹🌹🌹🙏🏼
محاسبه نیروی برآیند و کار نیروها در فیزیک دهم
پاسخ ها: {{ repliesNum }}
پاسخ انتخاب شده
در پاسخ به: {{ reply.reply_to.name }}
در پاسخ به
این پیام حذف شده است.