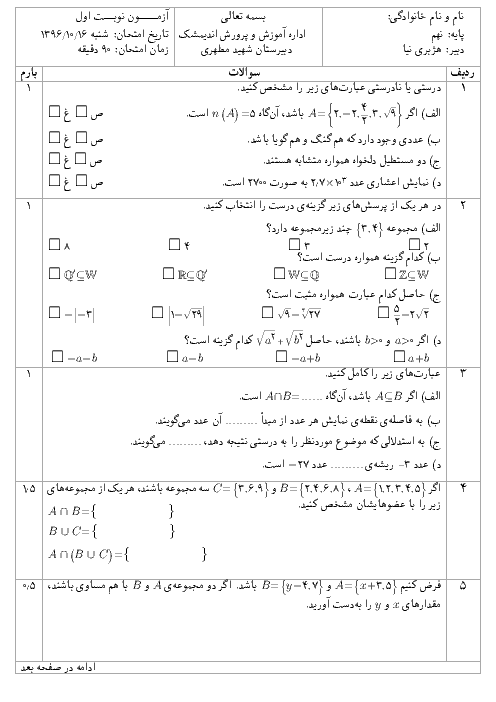
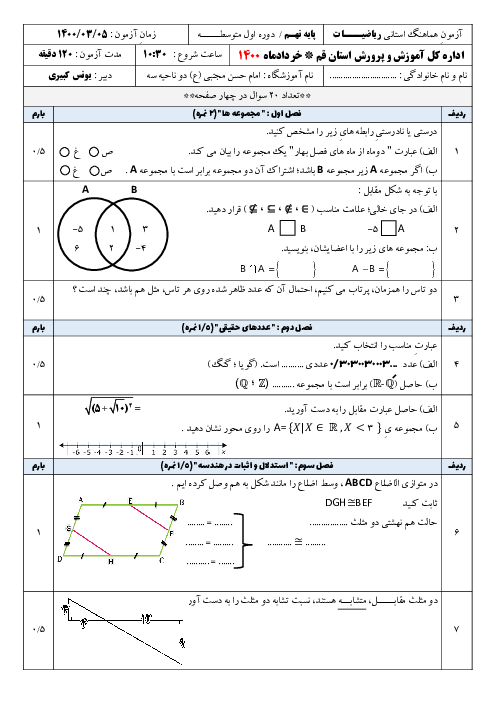
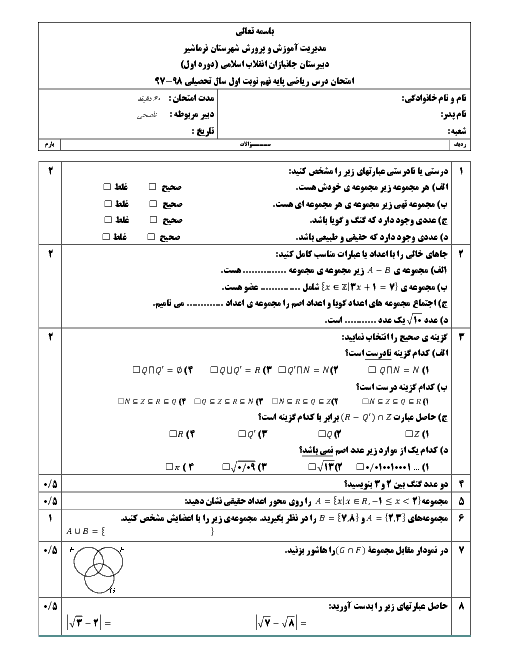
ممنون میشم این سوال رو توضیح بدید: اگر $(1+\sqrt{2})^8+(1-\sqrt{2})^8=1154$ باشد، بزرگترین عدد صحیح کوچتر از $(1+\sqrt{2})^8$ کدام است؟ الف) 1152 ب) 1153 ج) 1154 د) 1155 من اینجوری متوجه شدم ما بین دو عدد که توان زوج دارد جمع داریم، پس هیچ کدوم از این عدد های به توان رسیده منفی نیستن که تفریق در کار باشه. از آنجایی که $(1-\sqrt{2})$ عددی بین 0 و منفی یک هست، پس با به توان زوج رسیدن عددی بین 0 و 1 خواهد بود. حاصل جمع $(1+\sqrt{2})^8$ با عددی مثبت، 1154 شده است. در نتیجه $(1+\sqrt{2})^8$ قطعا از 1154 کمتر است. پس 1154 و 1155 نمی تواند بزرگترین عدد صحیح کوچکتر از $(1+\sqrt{2})^8$ باشد. از طرفی عددی که با $(1+\sqrt{2})^8$، جمع شده همان $(1-\sqrt{2})^8$، عددی بین 0 و 1 است، پس حاصل $(1+\sqrt{2})^8$ باید بین 1153 و 1154 باشد. اگر $(1+\sqrt{2})^8$ باید بین 1153 و 1154 باشد، بزرگترین عدد صحیح کوچتر از $(1+\sqrt{2})^8$ کدام است؟ گزینه ب) 1153
کدام گزینه درست است؟ با دلیل
پاسخ ها: {{ repliesNum }}
پاسخ انتخاب شده
در پاسخ به: {{ reply.reply_to.name }}
در پاسخ به
این پیام حذف شده است.