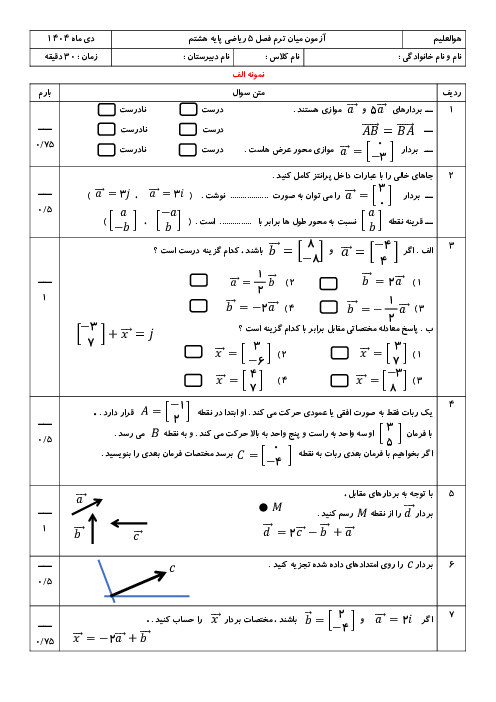
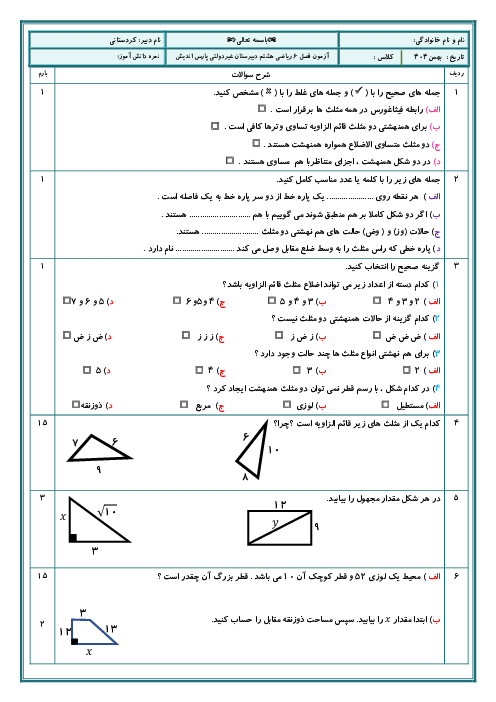
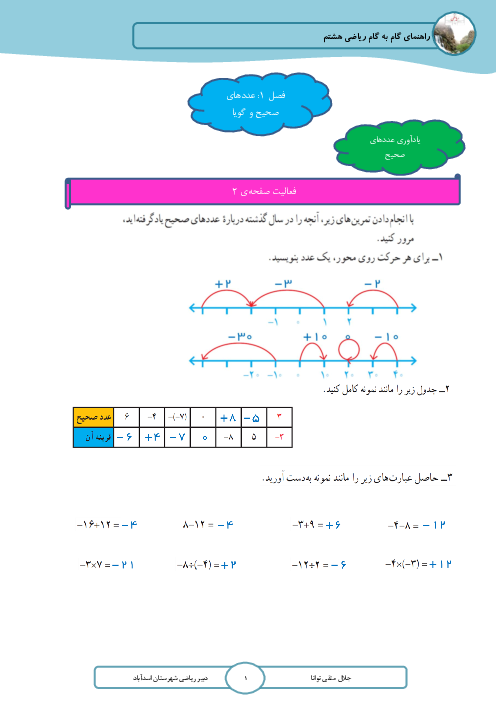
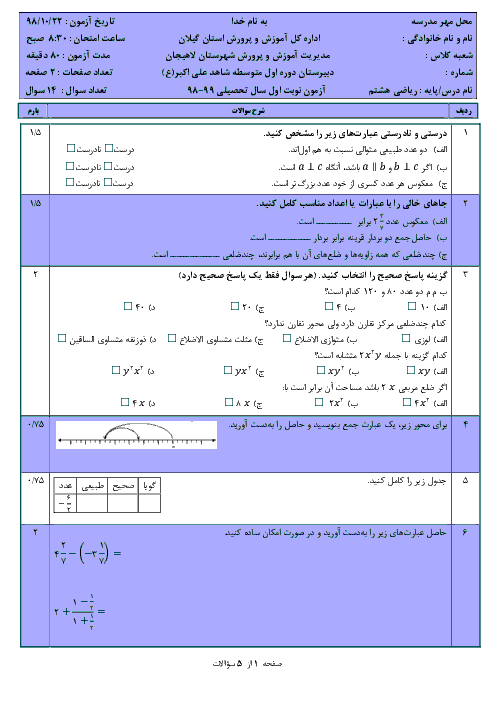
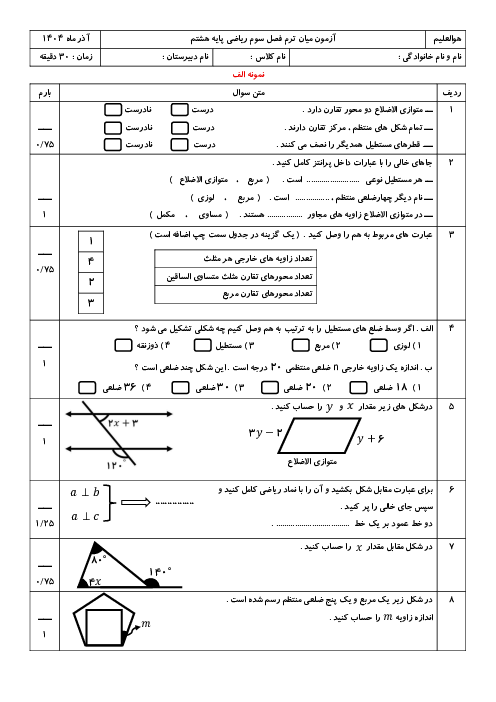
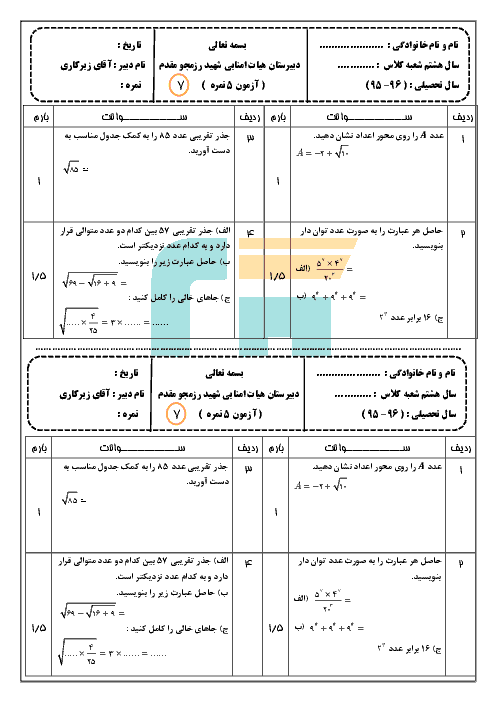
به حالت جبری ثابت کنید که حاصل ضرب دو عدد فرد یک عدد فرد می‌شود؟ - گاما

گاما رو نصب کن!

درحال دریافت اطلاعات ...

{{ successMsg }}

{{ errorMsg }}

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

قوانین و مقررات را خواندم و می پذیرم.

قبلا ثبت نام کرده اید؟ وارد شوید!

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد! )

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

ورود | ثبت نام

لطفا کمی صبر کنید ...

دوست خوبم!
برای نگهداری سابقه خریدتان، نیاز به شماره موبایل (یا ایمیل) شما داریم.

موبایل یا ایمیل

رمزعبور اگه یادت نیس نزن :)

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

ورود با رمزعبور

برای استفاده بسیاری از امکانات گاما و خیلی از وبسایت ها باید جاوا اسکریپت را در مرورگر خود فعال کنید.

برای این کار باید به تنظیمات مرورگر خود مراجعه کنید.

جستجو

پربازدیدها: #{{ tag.title }}

نمونه سوال

فایل آموزشی

پرسش و پاسخ

آزمون آنلاین

درسنامه آموزشی

مدرسه یاب

جستجوهای پرتکرار

نوبت دوم نمونه سوال گام به گام سوالات امتحان نهایی کاربرگ آزمون عملکردی پودمان آزمون پیشرفت تحصیلی طرح درس نوبت اول تست پاورپوینت علوم هشتم فارسی چهارم ریاضی هفتم علوم نهم

اگه میخوای سریع و کوتاه جواب بدی یه بسته بگیر!

لطفا برای پاسخ دادن شماره موبایل خود را تایید کنید.

فرم معتبر نیست.

نمونه سوال

محتوای آموزشی

آزمون آنلاین

پرسش و پاسخ

درسنامه آموزشی

مدرسه یاب

معلم خصوصی

تو بپرس ، بقیه بهت جواب میدن!

ASHI KING

بروزرسانی 22 فروردین 22:09

11 پرسش 1 پاسخ 3.8K امتیاز

دوره اول متوسطه هشتم ریاضی

به حالت جبری ثابت کنید که حاصل ضرب دو عدد فرد یک عدد فرد میشه و همچنین ثابت کنید که حاصل ضرب یک عدد زوج و یک عدد فرد یک عدد زوجج میشه

0

گزارش اشتراک گذاری

لطفا برای پاسخ دادن ابتدا وارد شوید. یا ثبت نام کنید.

جدید‌ترین پاسخ‌ها بهترین پاسخ‌ها

پاسخ ها: {{ repliesNum }}

{{ reply.name }}

بروزرسانی {{ reply.update_jalali }} {{ reply.subdate_jalali }}

{{ reply.stats.qNum }} پرسش {{ reply.stats.aNum }} پاسخ {{ reply.stats.score }} امتیاز

پاسخ انتخاب شده

در پاسخ به: {{ reply.reply_to.name }}

در پاسخ به

این پیام حذف شده است.

{{ reply.score }}

گزارش اشتراک گذاری

پاسخ صحیح لغو پاسخ صحیح ویرایش حذف پاسخ {{ (reply.reply_num > 0)? '(' + reply.reply_num + ')' : '' }}

سوپراستار

بسته ویژه نمره بیست: 5 نمونه سوال نوبت دوم ریاضی هشتم

22 صفحه

بسته ویژه نمره بیست: 5 نمونه سوال نوبت دوم ریاضی هشتم

ويژه نامه نوبت اول و…

سوپراستار

راهنمای گام به گام ریاضی هشتم | فصل های 1 تا 9

219 صفحه

راهنمای گام به گام ریاضی هشتم | فصل های 1 تا 9

جلال متقی توانا

رایـــــگان

آزمون نوبت دوم ریاضی هشتم همراه پاسخنامه تیزهوشان شهید باهنر کرج

4 صفحه

آزمون نوبت دوم ریاضی هشتم همراه پاسخنامه تیزهوشان شهید باهنر کرج

امیر قادری

رایـــــگان

دانلود نمونه سوال ریاضی پایه هشتم | فصل 1: عددهای صحیح و گویا

2 صفحه

دانلود نمونه سوال ریاضی پایه هشتم | فصل 1: عددهای صحیح و گویا

جمشید فروغی

آزمون نوبت اول ریاضی هشتم دبیرستان غیردولتی میرداماد | مرداد 93

4 صفحه

آزمون نوبت اول ریاضی هشتم دبیرستان غیردولتی میرداماد | مرداد 93

مجتبی دایی

آزمون نوبت اول ریاضی هشتم دبیرستان دوره اول مشکات تبریز در دیماه 1402

6 صفحه

آزمون نوبت اول ریاضی هشتم دبیرستان دوره اول مشکات تبریز در دیماه 1402

حسن نعمتیان

امتحان ریاضی هشتم مدرسه شاهد حضرت علی اکبر | فصل 4: جبر و معادله

4 صفحه

امتحان ریاضی هشتم مدرسه شاهد حضرت علی اکبر | فصل 4: جبر و معادله

محمد پاک نژاد

نمونه سوال امتحان نوبت دوم خرداد 1402 ریاضی هشتم مدرسه حجاب

4 صفحه

نمونه سوال امتحان نوبت دوم خرداد 1402 ریاضی هشتم مدرسه حجاب

مریم گودرزی

رایـــــگان

آزمون پایانی نوبت اول ریاضی هشتم - تا پایان فصل پنجم

3 صفحه

آزمون پایانی نوبت اول ریاضی هشتم - تا پایان فصل پنجم

جمشید فروغی

رایـــــگان

تمرین در خانه ریاضی هشتم | فصل چهارم: جبر و معادله

2 صفحه

تمرین در خانه ریاضی هشتم | فصل چهارم: جبر و معادله

محیا کوشکستانی