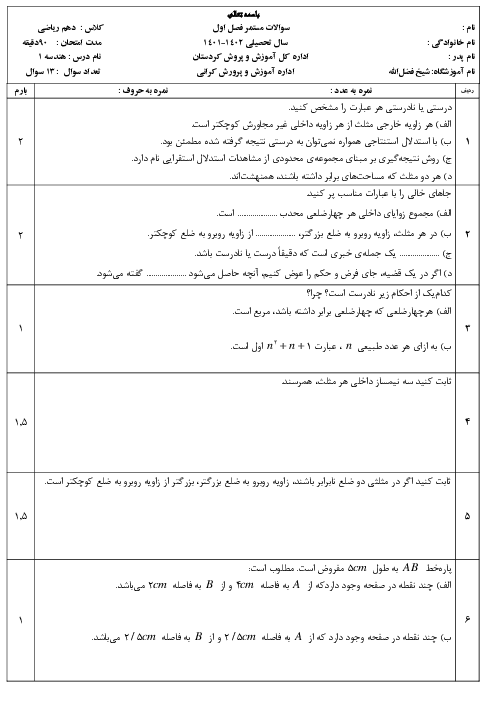
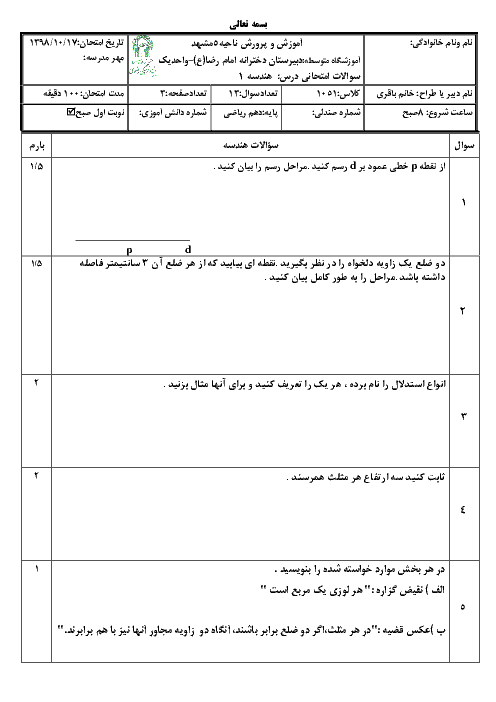
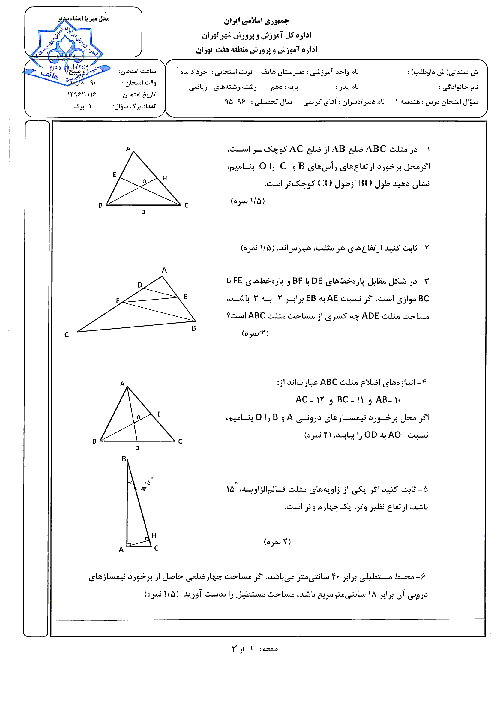
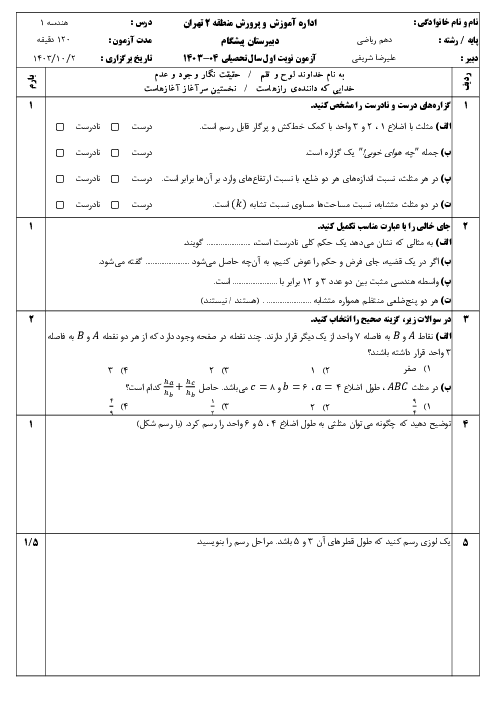
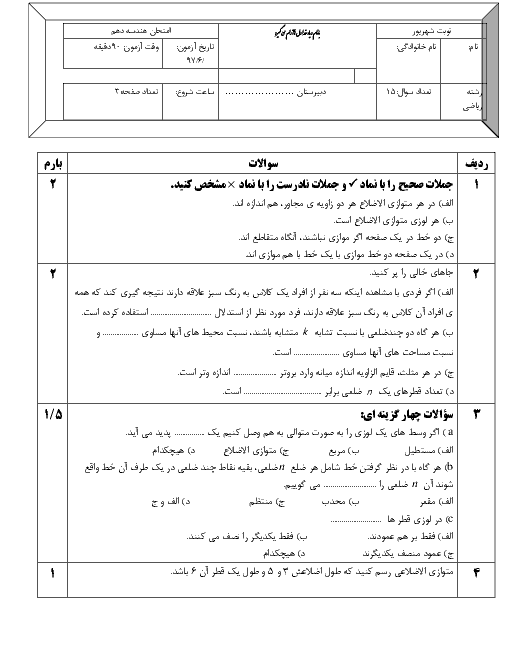
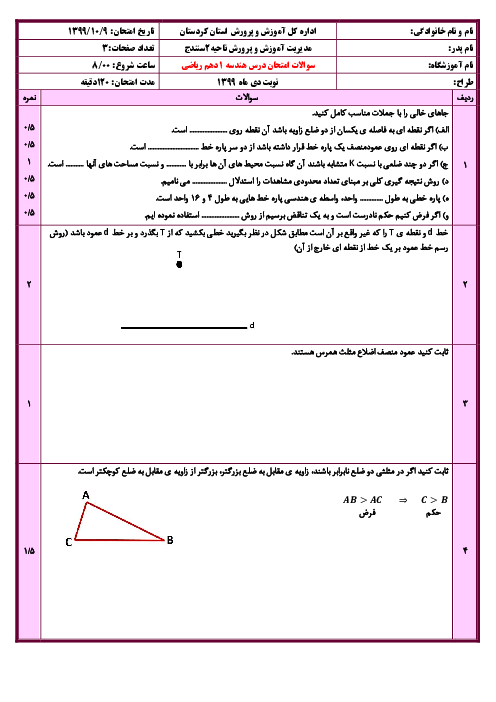
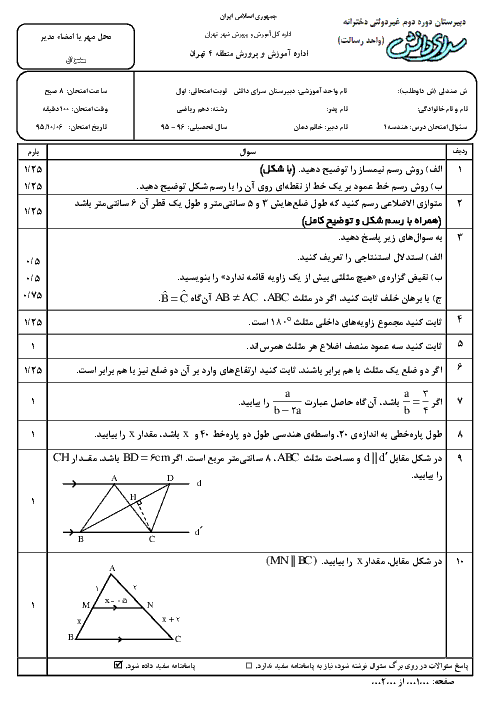
ثابت کنید اگر دو زاویه از مثلثی باهم برابر باشند آن مثلث متساوی الساقین است. - گاما

گاما رو نصب کن!

برای استفاده بسیاری از امکانات گاما و خیلی از وبسایت ها باید جاوا اسکریپت را در مرورگر خود فعال کنید.

برای این کار باید به تنظیمات مرورگر خود مراجعه کنید.

جستجو

پربازدیدها: #{{ tag.title }}

نمونه سوال

فایل آموزشی

پرسش و پاسخ

آزمون آنلاین

درسنامه آموزشی

مدرسه یاب

جستجوهای پرتکرار

گام به گام نوبت اول کاربرگ آزمون عملکردی پودمان آزمون پیشرفت تحصیلی طرح درس نمونه سوال تست پاورپوینت علوم هشتم فارسی چهارم ریاضی هفتم علوم نهم گزارش کارورزی

اگه میخوای سریع و کوتاه جواب بدی یه بسته بگیر!

لطفا برای پاسخ دادن ابتدا وارد شوید. یا ثبت نام کنید.

نمونه سوال

محتوای آموزشی

آزمون آنلاین

پرسش و پاسخ

درسنامه آموزشی

مدرسه یاب

معلم خصوصی

تو بپرس ، بقیه بهت جواب میدن!

Mohammad Ash

بروزرسانی 8 مرداد 12:12

1 پرسش 0 پاسخ 3.1K امتیاز

دوره دوم متوسطه- نظری دهم علوم ریاضی هندسه (1)

ثابت کنید اگر دوزاویه از مثلثی باهم برابر باشند آن مثلث متساوی الساقین است

3

گزارش اشتراک گذاری

لطفا برای پاسخ دادن ابتدا وارد شوید. یا ثبت نام کنید.

جدید‌ترین پاسخ‌ها بهترین پاسخ‌ها

پاسخ ها: {{ repliesNum }}

{{ reply.name }}

بروزرسانی {{ reply.update_jalali }} {{ reply.subdate_jalali }}

{{ reply.stats.qNum }} پرسش {{ reply.stats.aNum }} پاسخ {{ reply.stats.score }} امتیاز

پاسخ انتخاب شده

در پاسخ به: {{ reply.reply_to.name }}

در پاسخ به

این پیام حذف شده است.

{{ reply.score }}

گزارش اشتراک گذاری

پاسخ صحیح لغو پاسخ صحیح ویرایش حذف پاسخ {{ (reply.reply_num > 0)? '(' + reply.reply_num + ')' : '' }}

سوپراستار

کلید طلایی نمره 20 در امتحان هماهنگ کشوری هندسه 1 دهم رشته ریاضی فیزیک

67 صفحه

کلید طلایی نمره 20 در امتحان هماهنگ کشوری هندسه 1 دهم رشته ریاضی فیزیک

مژگان موسویان

سوالات آزمون نوبت دوم هندسه (1) دهم دبیرستان امام خمینی کرج | خرداد 1400

5 صفحه

سوالات آزمون نوبت دوم هندسه (1) دهم دبیرستان امام خمینی کرج | خرداد 1400

مجتبی خالقی

رایـــــگان

امتحان درس ترسیم‌های هندسی | هندسه (1) دهم دبیرستان شهید نجفی رودسر

4 صفحه

امتحان درس ترسیم‌های هندسی | هندسه (1) دهم دبیرستان شهید نجفی رودسر

اسدالله رضازاده

آزمون نوبت دوم هندسه (1) دهم دبیرستان جاویدان | خرداد 1398

2 صفحه

آزمون نوبت دوم هندسه (1) دهم دبیرستان جاویدان | خرداد 1398

حسین زنجانی

امتحان ترم دوم هندسه (1) دهم دبیرستان فرزانگان یزد | خرداد 1401

4 صفحه

امتحان ترم دوم هندسه (1) دهم دبیرستان فرزانگان یزد | خرداد 1401

نرگس نوفرد

سوالات امتحان نوبت اول هندسه (1) دهم رشته رياضی دبیرستان نمونه دولتی شهرستان انار - دی 95

3 صفحه

سوالات امتحان نوبت اول هندسه (1) دهم رشته رياضی دبیرستان نمونه دولتی شهرستان…

محمد معین آقازاده

امتحان ترم اول هندسه دهم رشته ریاضی دبیرستان فرزانگان 2 تهران | دی 98

4 صفحه

امتحان ترم اول هندسه دهم رشته ریاضی دبیرستان فرزانگان 2 تهران | دی 98

امتحان دهمی ها

تمرین های پاسخ دار هندسه (1) دهم | فصل 1: ترسیم‌های هندسی و استدلال

11 صفحه

تمرین های پاسخ دار هندسه (1) دهم | فصل 1: ترسیم‌های هندسی و استدلال

علی فقیهی

امتحان نوبت اول هندسه (1) دهم رشته رياضی دبیرستان نمونه پیامبر اعظم (ص) شهرستان سیب سوران | دی 95

2 صفحه

امتحان نوبت اول هندسه (1) دهم رشته رياضی دبیرستان نمونه پیامبر اعظم (ص)…

محمد معین آقازاده

آزمون نوبت دوم هندسه (1) پایه دهم دبیرستان ماندگار شیخ صدوق | خرداد 1396

5 صفحه

آزمون نوبت دوم هندسه (1) پایه دهم دبیرستان ماندگار شیخ صدوق | خرداد 1396

مسلم آقازاده