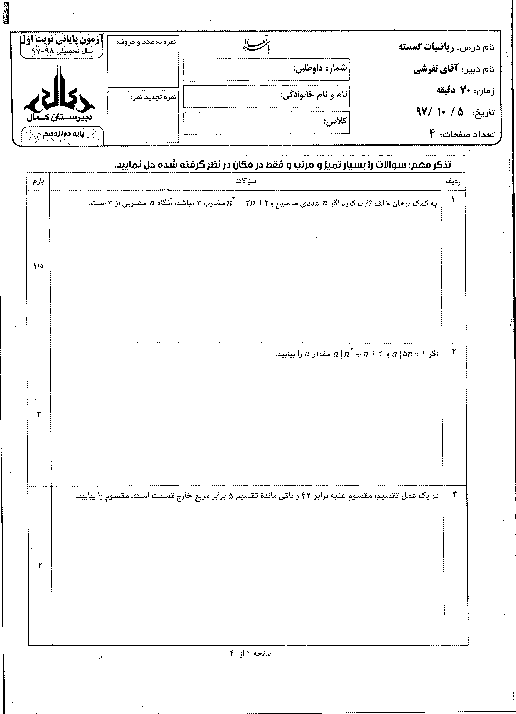
سه به توان سه میشه 27 و عدد 27 با 3- همنهشت هست به پیمانه 15 و ....
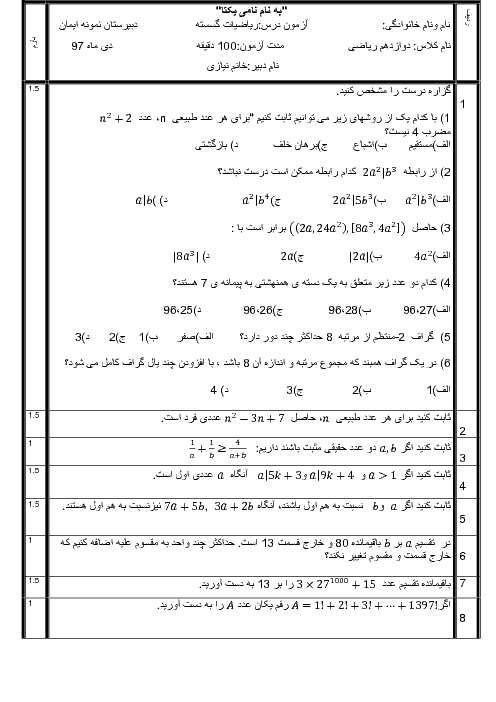
باقیمانده تقسیم 3 به توان 100 را بر 15 به دست آورید.
پاسخ ها: {{ repliesNum }}
پاسخ انتخاب شده
در پاسخ به: {{ reply.reply_to.name }}
در پاسخ به
این پیام حذف شده است.