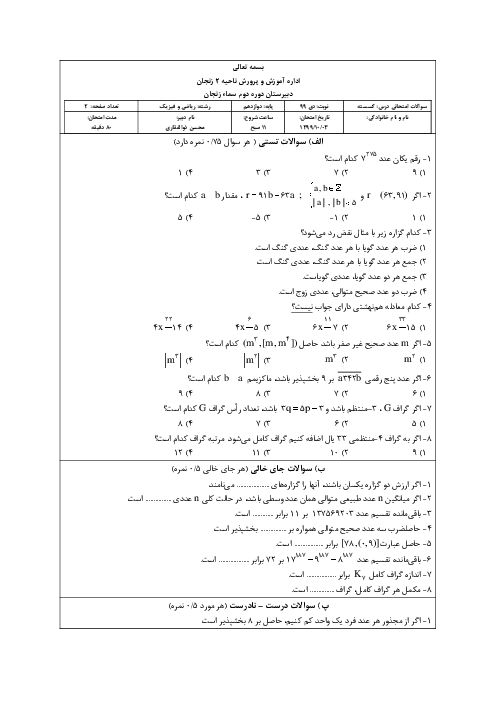
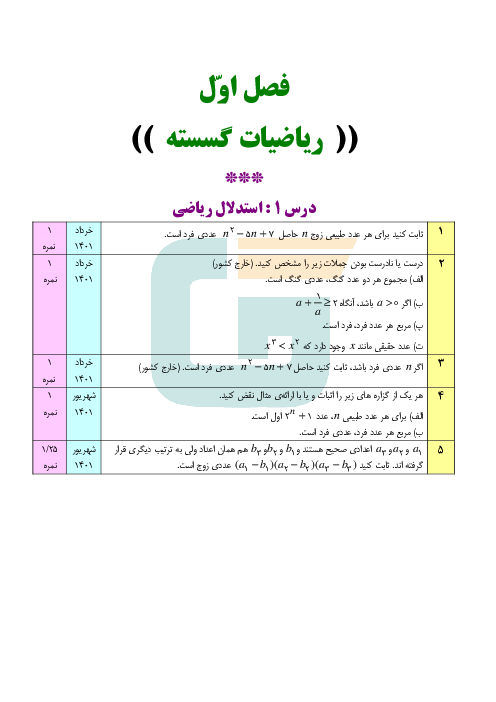
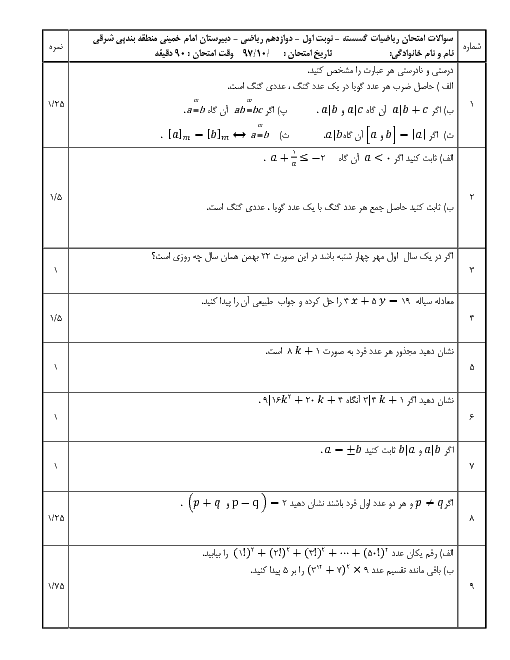
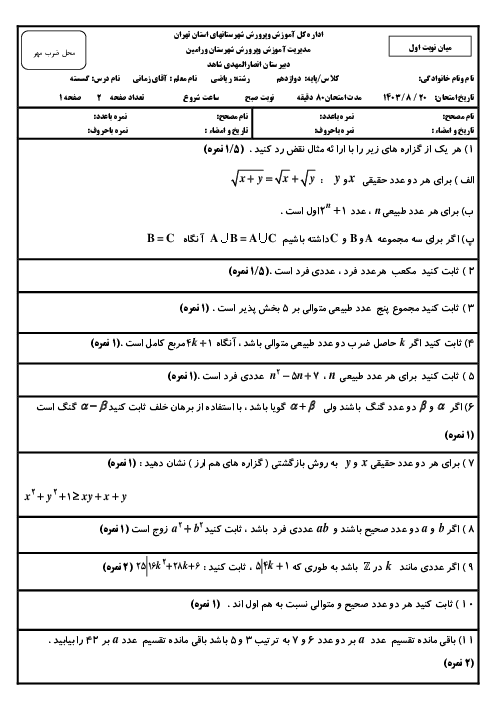
توجه داشته باشید هر عدد فرد به صورت 4k+1یا 4k+3 است .
ثابت کنید مربع هر عدد فرد در تقسیم بر 8 دارای باقی مانده 1 میشود.
پاسخ ها: {{ repliesNum }}
پاسخ انتخاب شده
در پاسخ به: {{ reply.reply_to.name }}
در پاسخ به
این پیام حذف شده است.