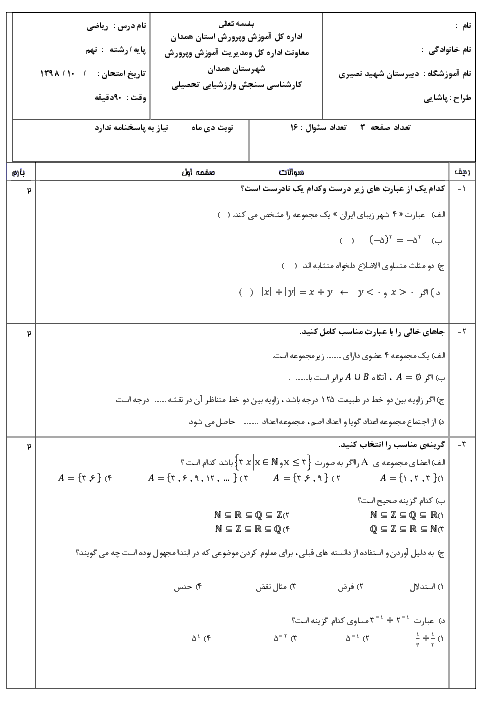
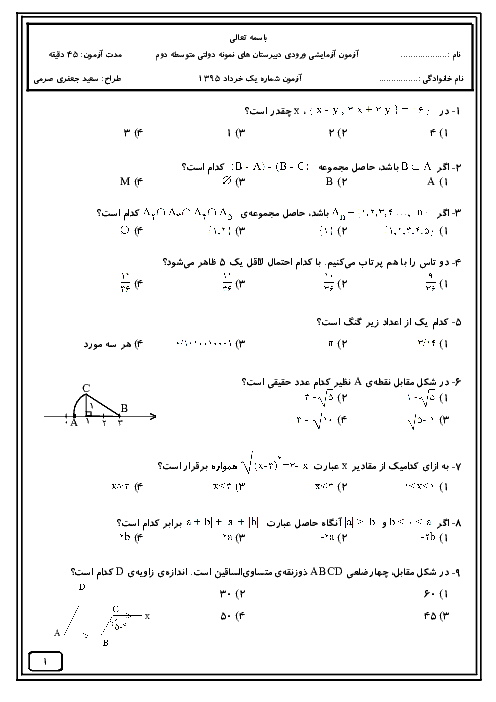
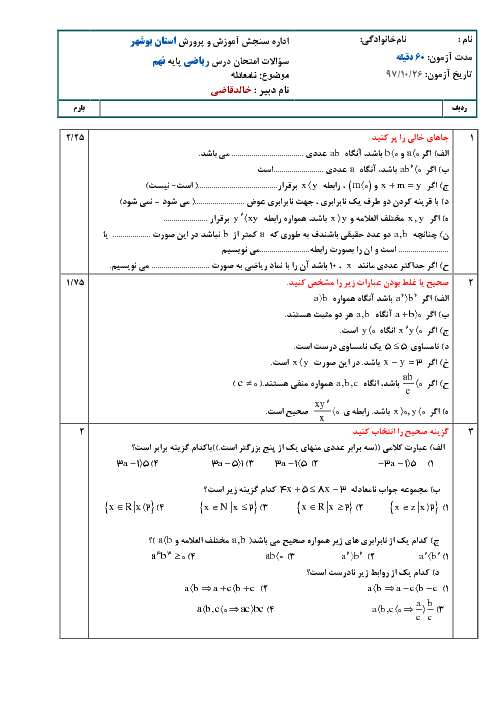
اثبات کنید: $\frac{a}{b} \lt \frac{a+c}{b+d} \lt \frac{c}{d}$
جدیدترین پاسخها
بهترین پاسخها
![]()
پاسخ ها: {{ repliesNum }}
پاسخ انتخاب شده
در پاسخ به: {{ reply.reply_to.name }}
در پاسخ به
این پیام حذف شده است.