درسنامه آموزشی فصل اول ریاضی کلاس هفتم | مرور راهبردها با پاسخ - گاما

گاما رو نصب کن!

برای استفاده بسیاری از امکانات گاما و خیلی از وبسایت ها باید جاوا اسکریپت را در مرورگر خود فعال کنید.

برای این کار باید به تنظیمات مرورگر خود مراجعه کنید.

جستجو

پربازدیدها: #{{ tag.title }}

نمونه سوال

فایل آموزشی

پرسش و پاسخ

آزمون آنلاین

درسنامه آموزشی

مدرسه یاب

جستجوهای پرتکرار

گام به گام نوبت اول کاربرگ آزمون عملکردی پودمان آزمون پیشرفت تحصیلی طرح درس نمونه سوال تست پاورپوینت علوم هشتم فارسی چهارم ریاضی هفتم علوم نهم گزارش کارورزی

نمونه سوال

محتوای آموزشی

آزمون آنلاین

پرسش و پاسخ

درسنامه آموزشی

مدرسه یاب

معلم خصوصی

درحال دریافت اطلاعات ...

آخرین ویرایش: {{ views }} اشتراک گزارش خطا

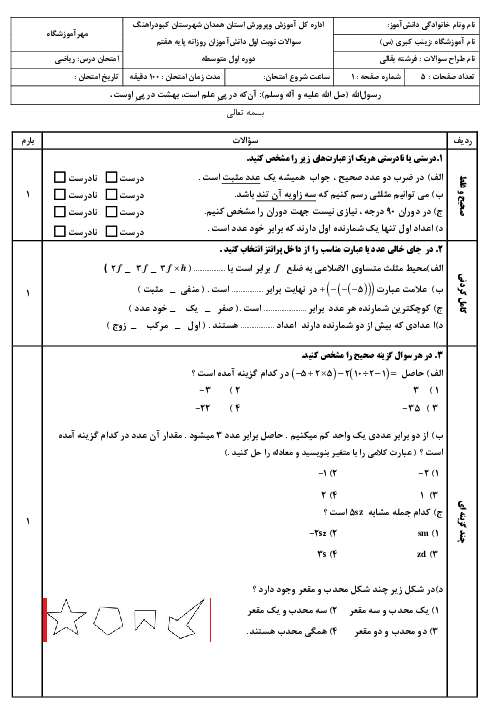
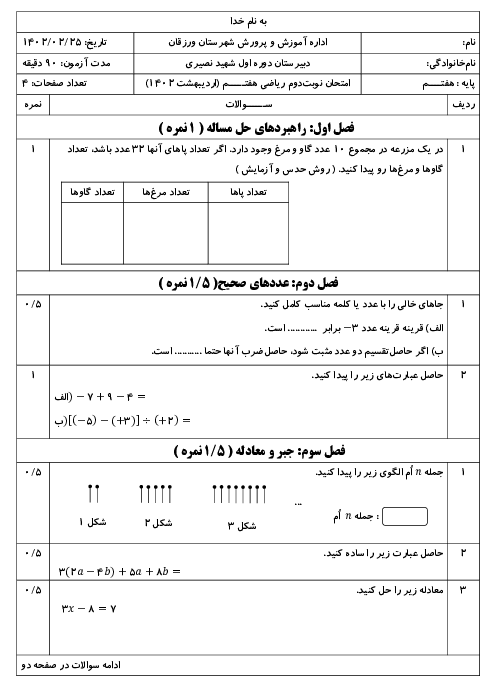
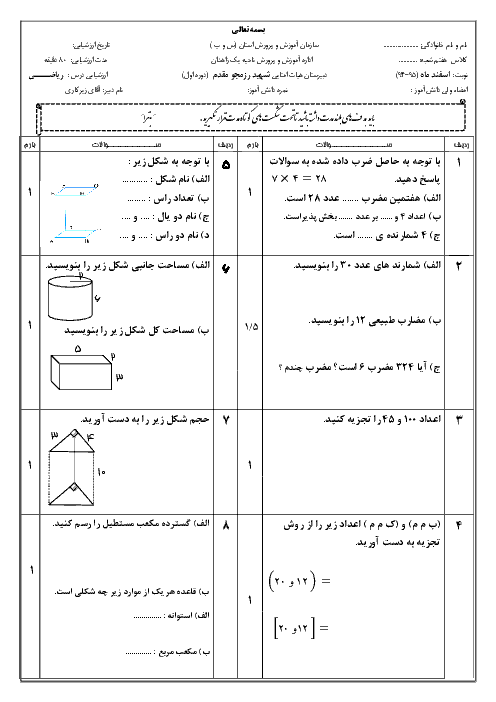
ریاضی
- فصل 1: راهبردهای حل مسئله
- راهبرد رسم شکل
- راهبرد الگوسازی
- راهبرد حذف حالت‌های نامطلوب
- راهبرد الگویابی
- راهبرد حدس و آزمایش
- راهبرد زیرمسئله
- راهبرد حل مسئله ساده‌تر
- راهبرد روش‌های نمادین
- مرور راهبردها
- فصل 2: عددهای صحیح
- درس 1: معرفی عددهای علامت‌دار
- درس 2: جمع و تفریق عددهای صحیح (1)
- درس 3: جمع و تفریق عددهای صحیح (2)
- درس 4: ضرب و تقسیم عددهای صحیح
- فصل 3: جبر و معادله
- درس 1: الگوهای عددی
- درس 2: عبارت‌های جبری
- درس 3: مقدار عددی یک عبارت جبری
- درس 4: معادله
- فصل 4: هندسه و استدلال
- درس 1: روابط بین پاره خط‌ها
- درس 2: روابط بین زاویه‌ها
- درس 3: تبدیلات هندسی (انتقال، تقارن، دوران)
- درس 4: شکل‌های مساوی (هم‌نهشت)
- فصل 5: شمارنده‌ها و اعداد اول
- درس 1: عدد اول
- درس 2: شمارندهٔ اول
- درس 3: بزرگ‌ترین شمارنده مشترک
- درس 4: کوچک‌ترین مضرب مشترک
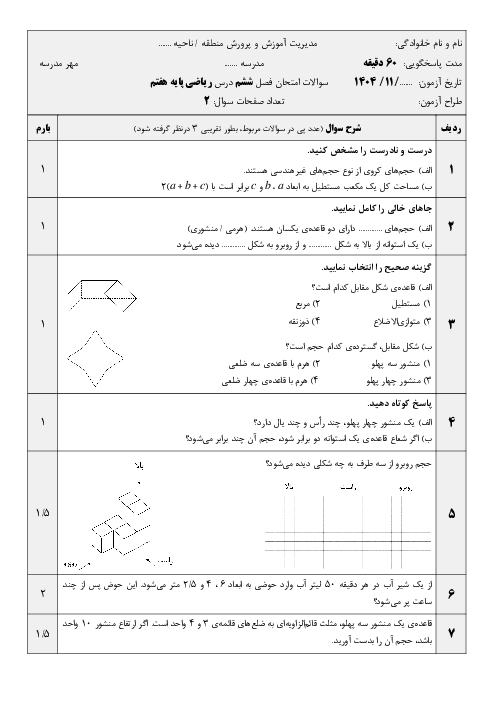
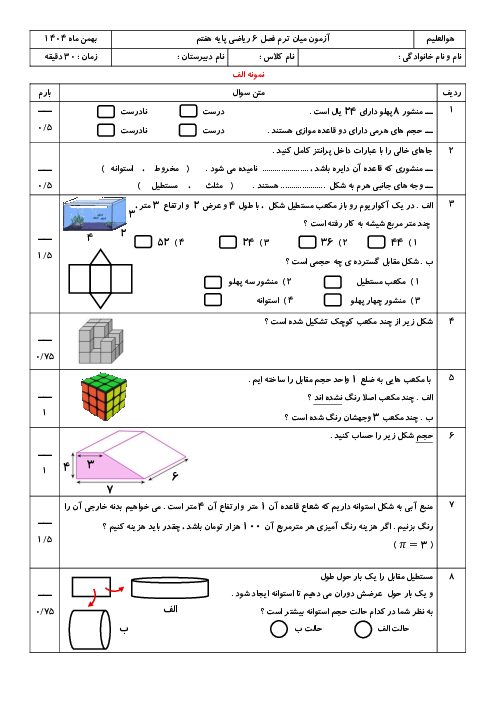
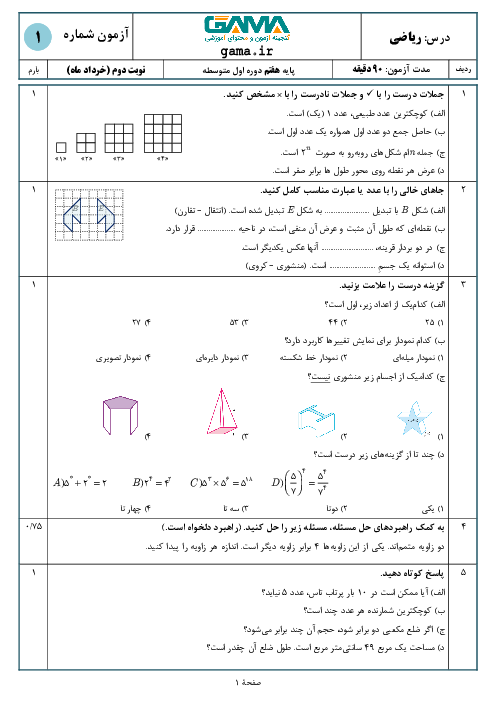
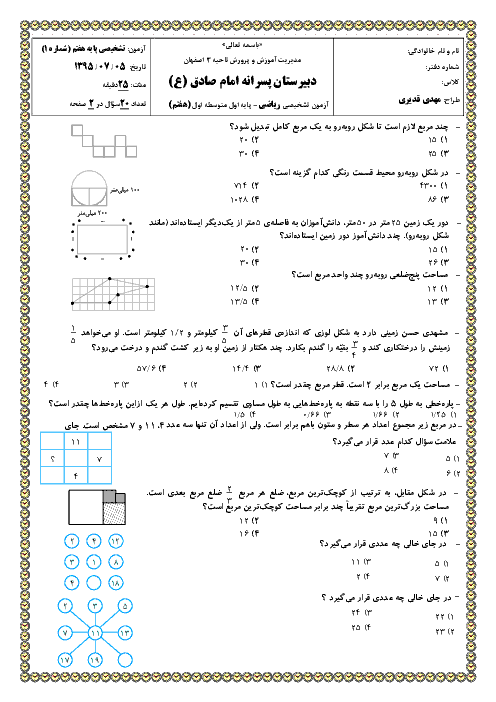
- فصل 6: سطح و حجم
- درس 1: حجم‌های هندسی
- درس 2: محاسبهٔ حجم‌های منشوری
- درس 3: مساحت جانبی و کل
- درس 4: حجم و سطح
- فصل 7: توان و جذر
- درس 1: تعریف توان
- درس 2: محاسبهٔ عبارت‌ توان‌دار
- درس 3: ساده کردن عبارت‌های توان‌‌دار
- درس 4: جذر و ریشه
- فصل 8: بردار و مختصات
- درس 1: پاره‌خط جهت دار
- درس 2: بردارهای مساوی و قرینه
- درس 3: مختصات
- درس 4: بردار انتقال
- فصل 9: آمار و احتمال
- درس 1: جمع‌آوری و نمایش داده‌ها
- درس 2: نمودارها و تفسیر نتیجه‌ها
- درس 3: احتمال یا اندازه‌گیری شانس
- درس 4: احتمال و تجربه

ویدیو دوره آموزشی، ریاضی هفتم دوره اول متوسطه

مدرس: محمودرضا میرزایی

مدت دوره: 44 ساعت (61 فایل)

با آلبوم تست، آزمون دلخواهتو بساز

سوپراستار

بسته ویژه نمره بیست: 5 نمونه سوال نوبت دوم ریاضی هفتم

27 صفحه

بسته ویژه نمره بیست: 5 نمونه سوال نوبت دوم ریاضی هفتم

ويژه نامه نوبت اول و…

سوپراستار

5 سری مجموعه سوالات امتحان حساب پایه‌ی هفتم مدرسه سلام يوسف آباد | فصل های 1 و 2 و 3 و 5 و 7

15 صفحه

5 سری مجموعه سوالات امتحان حساب پایه‌ی هفتم مدرسه سلام يوسف آباد | فصل…

مرتضی جمالی ابیانه

رایـــــگان

100 تمرین اولویت محاسبات ریاضی

6 صفحه

100 تمرین اولویت محاسبات ریاضی

حسین سلطانی

آزمون ترم اول ریاضی هفتم مدرسه شهید برادران ستوده | دی 1398

3 صفحه

آزمون ترم اول ریاضی هفتم مدرسه شهید برادران ستوده | دی 1398

حسن سلیمی

رایـــــگان

آزمون ریاضی هفتم دبیرستان شهید اژه‌ ای اصفهان | فصل 1 و 2

3 صفحه

آزمون ریاضی هفتم دبیرستان شهید اژه‌ ای اصفهان | فصل 1 و 2

مهدی قدیری

آزمون ریاضی هفتم | راهبردهای حل مساله

5 صفحه

آزمون ریاضی هفتم | راهبردهای حل مساله

الهام حبیبیان

امتحان نوبت اول ریاضی هفتم دبیرستان هیات امنایی حافظ سنندج | فصل 1 ت 5

4 صفحه

امتحان نوبت اول ریاضی هفتم دبیرستان هیات امنایی حافظ سنندج | فصل 1 ت 5

شیرین شاهانی

راهنمای گام به گام ریاضی هفتم | فصل 1 تا 9

173 صفحه

راهنمای گام به گام ریاضی هفتم | فصل 1 تا 9

جلال متقی توانا

امتحان نوبت اول ریاضی هفتم دبیرستان دخترانه میثاق | دی 1401

6 صفحه

امتحان نوبت اول ریاضی هفتم دبیرستان دخترانه میثاق | دی 1401

محمدرضا غفارزاده

آزمون نوبت اول ریاضی هفتم دبیرستان فرزانگان ساوجبلاغ | دی 98

3 صفحه

آزمون نوبت اول ریاضی هفتم دبیرستان فرزانگان ساوجبلاغ | دی 98

آیت کریمی

موارد بیشتر

موارد بیشتر

ارسال فایل

مریم از دو برابر سن زهرا 10 سال کوچکتر است، اگر مریم 15 سال از زهرا بزرگتر باشد، سن هر دو را بدست آورید.

مستطیلی که طولش 6 وعرضش 10 است حول ضلعABدوران کرده است نام شکل وحجم حاصل رابدست آورید لطفاً سریع جواب بدید ممنونم

طول هر ضلع قاعده چند سانتی‌متر است؟

موارد بیشتر

ارسال پرسش

موارد بیشتر