ذره‌ای با بار الکتریکی با تندی وارد میدان مغناطیسی یکنواخت (در SI) شده و از طرف میدان به ذره نیرویی به اندازهٔ وارد می‌شود. زاویهٔ بردار سرعت ذره با بردار میدان…

موبایل / ایمیل

لطفا کدی که به {{ identity }} ارسال شده است را وارد کنید.

کد فعال سازی :

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

لطفا برای حساب خود رمز عبور انتخاب کنید.

رمزعبور :

تکرار رمزعبور :

قوانین و مقررات را خواندم و می پذیرم.

قبلا ثبت نام کرده اید؟ وارد شوید!

موبایل / ایمیل

لطفا کدی که برای شما ارسال شده است را وارد کنید.

کد فعال سازی :

ارسال مجدد کد فعال سازی {{ countDown }}

منتظر دریافت پیامک شما ...

برای حساب خود رمز عبور جدید انتخاب کنید.

رمزعبور :

تکرار رمزعبور :

ورود | ثبت نام

لطفا کمی صبر کنید ...

موبایل / ایمیل

رمزعبور

رمز عبور خود را فراموش کردید؟ بازیابی کنید.

هنوز عضو نشده اید؟ ثبت نام کنید.

گزینه انتخاب شده در پاسخنامه درست نیست.

بیش از یک گزینه درست وجود دارد.

هیچ گزینه ای درست نیست.

اشکال تایپی در صورت سوال یا در گزینه ها وجود دارد.

این تست با تست دیگری در همین آزمون تشابه دارد.

در پاسخ تشریحی اشکال وجود دارد.

این تست خارج از بودجه بندی یا مبحث مورد نظر است.

سایر موارد

حداقل 25 کاراکتر باید وارد کنید.

قسمت 3: نیروی مغناطیسی وارد بر ذرّۀ باردار متحرک در میدان مغناطیسی فیزیک (2) یازدهم دوره دوم متوسطه- نظری علوم تجربی درسنامه آموزشی این مبحث

ذره‌ای با بار الکتریکی $+0/5\mu C$ با تندی $2\times {{10}^{5}}\frac{m}{s}$ وارد میدان مغناطیسی یکنواخت $\overrightarrow{B}=4(\overrightarrow{i}+\overrightarrow{j})$ (در SI) شده و از طرف میدان به ذره نیرویی به اندازهٔ $0/4N$ وارد می‌شود. زاویهٔ بردار سرعت ذره با بردار میدان مغناطیسی چند درجه می‌تواند باشد؟

1 )

2 )

3 )

4 )

نمایش پاسخ

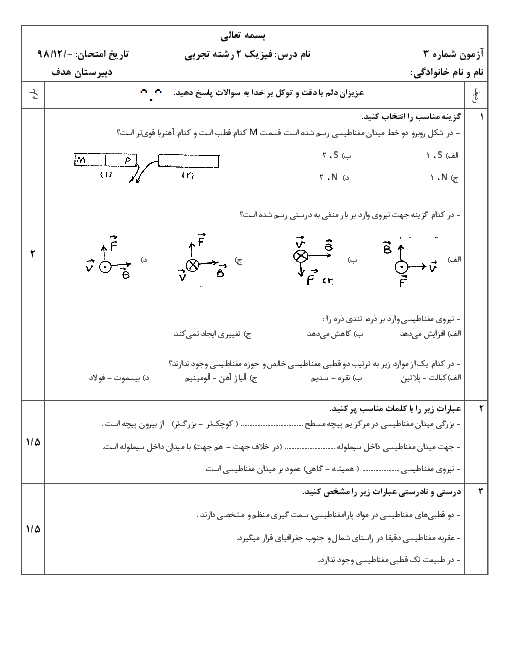
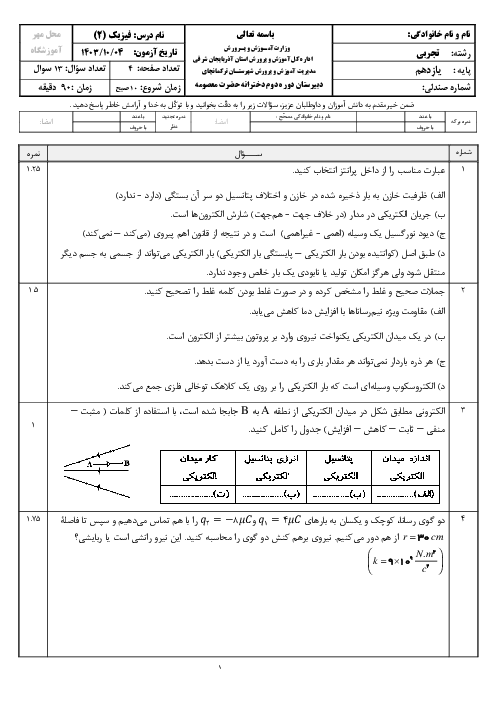
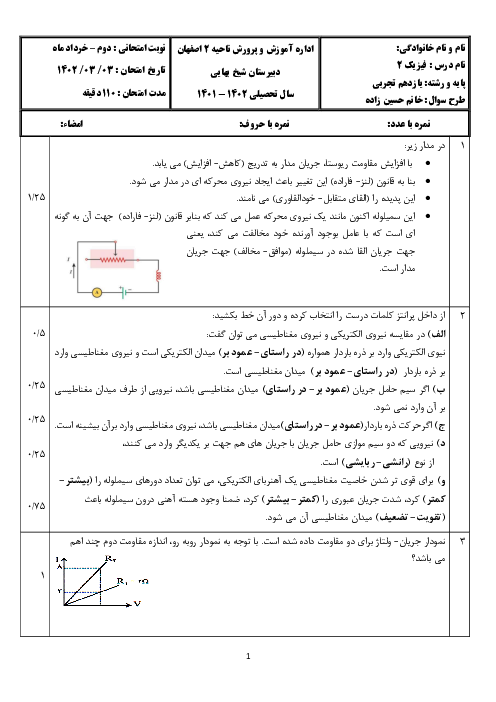
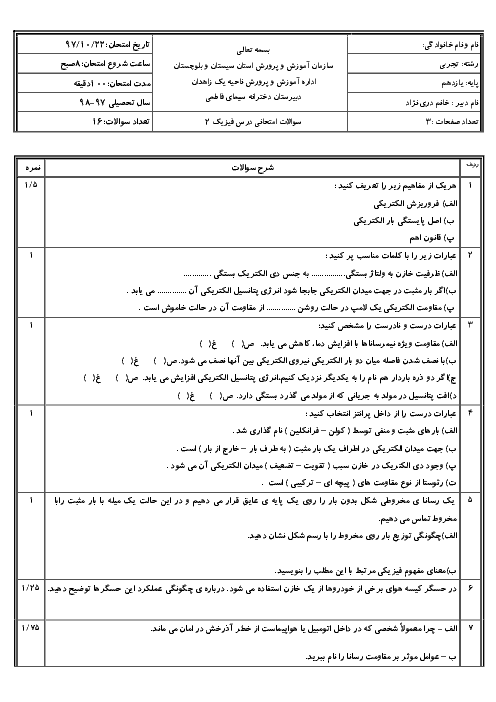
ابتدا با داشتن بردار ميدان مغناطيسی، بزرگی ميدان را محاسبه می‌كنيم.

$\overrightarrow{B}=\overrightarrow{4i}+\overrightarrow{4j}\Rightarrow \left| \overrightarrow{B} \right|=\sqrt{{{4}^{2}}+{{4}^{2}}}=\sqrt{2\times {{4}^{2}}}=4\sqrt{2}T$

اكنون از رابطهٔ نيروی مغناطيسی وارد بر ذرهٔ باردار متحرک درون ميدان مغناطيسی كمک می‌گيريم و زاويهٔ بردار سرعت ذره با بردار ميدان را به‌دست می‌آوريم.

$\left| \overrightarrow{F} \right|=qvB\,\sin \theta $

$\Rightarrow 0/4=0/5\times {{10}^{-6}}\times 2\times {{10}^{5}}\times 4\sqrt{2}\times \sin \theta $

$\Rightarrow \sin \theta =\frac{\sqrt{2}}{2}\Rightarrow \theta ={{450}^{\circ }}$ یا $\theta ={{135}^{\circ }}$

گزارش اشکال