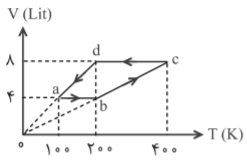
ابتدا كار انجام شده بر روی گاز در هر يک ازفرايندها را به صورت زير حساب می‌کنیم. چون فرایندهای $ab$ و $cd$ هم‌حجم‌اند، ${{W}_{ab}}={{W}_{cd}}=0$ می‌باشد. برای فرايندهای $bc$ و $da$ ، چون نمودار خطی دارند و امتداد این فرایندها از مبدأ مختصات می‌گذرند این دو فرایند هم‌فشارند و می‌توان نوشت:

${{W}_{bc}}=-nR({{T}_{c}}-{{T}_{b}})\xrightarrow[n=1mol\,\,,\,\,R=8\frac{J}{mol.K}]{{{T}_{c}}=400K\,\,,\,\,{{T}_{b}}=200K}$

${{W}_{bc}}=-1\times 8\times (400-200)\Rightarrow {{W}_{bc}}=-1600J$

${{W}_{da}}=-nR({{T}_{a}}-{{T}_{d}})\xrightarrow[n=1mol]{{{T}_{a}}=100K\,\,,\,\,{{T}_{d}}=200K}$

${{W}_{da}}=-1\times 8\times (100-200)\Rightarrow {{W}_{da}}=800J$

اکنون با استفاده از مجموع کار هر یک از فرایندها، کار انجام شده در طی چرخه را به دست می‌آوریم و سپس با استفاده از قانون اول ترمودینامیک، $Q$ را حساب می‌کنیم.

${{W}_{T}}={{W}_{ab}}+{{W}_{bc}}+{{W}_{cd}}+{{W}_{da}}$

$\xrightarrow[{{W}_{bc}}=-1600J\,\,,\,\,{{W}_{da}}=800J]{{{W}_{ab}}={{W}_{cd}}=0}$

${{W}_{T}}=0-1600+800\Rightarrow {{W}_{T}}=-800J$

$\Delta U={{W}_{T}}+{{Q}_{T}}\xrightarrow{\Delta U=0}0=-800+{{Q}_{T}}\Rightarrow {{Q}_{T}}=800J$