اگر مضرب باشد؛ ولی مضرب نباشد، آنگاه به كدام‌يك از صورت‌های زير نوشته می‌شود؟ | ریاضیات گسسته دوازدهم شماره 79781 - گاما

گاما رو نصب کن!

درحال دریافت اطلاعات ...

{{ successMsg }}

{{ errorMsg }}

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

قوانین و مقررات را خواندم و می پذیرم.

قبلا ثبت نام کرده اید؟ وارد شوید!

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد! )

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

ورود | ثبت نام

لطفا کمی صبر کنید ...

دوست خوبم!
برای نگهداری سابقه خریدتان، نیاز به شماره موبایل (یا ایمیل) شما داریم.

موبایل یا ایمیل

رمزعبور اگه یادت نیس نزن :)

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

ورود با رمزعبور

برای استفاده بسیاری از امکانات گاما و خیلی از وبسایت ها باید جاوا اسکریپت را در مرورگر خود فعال کنید.

برای این کار باید به تنظیمات مرورگر خود مراجعه کنید.

جستجو

پربازدیدها: #{{ tag.title }}

نمونه سوال

فایل آموزشی

پرسش و پاسخ

آزمون آنلاین

درسنامه آموزشی

مدرسه یاب

جستجوهای پرتکرار

نوبت اول گام به گام کاربرگ آزمون عملکردی پودمان آزمون پیشرفت تحصیلی طرح درس نمونه سوال تست پاورپوینت علوم هشتم فارسی چهارم ریاضی هفتم علوم نهم گزارش کارورزی

نمونه سوال

محتوای آموزشی

آزمون آنلاین

پرسش و پاسخ

درسنامه آموزشی

مدرسه یاب

معلم خصوصی

فرم معتبر نیست.

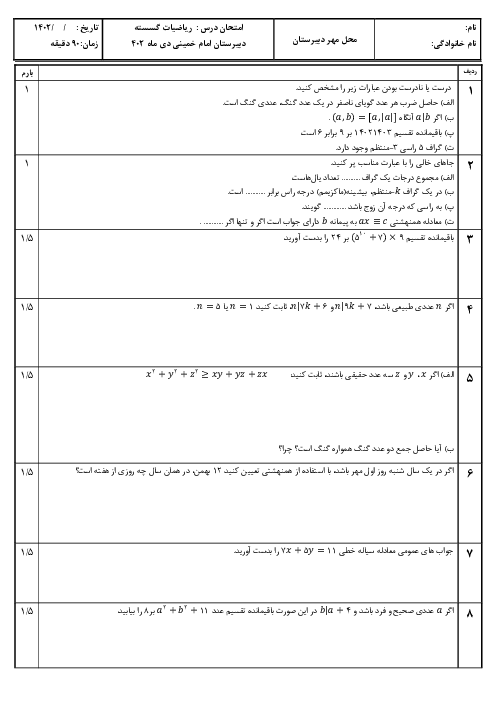
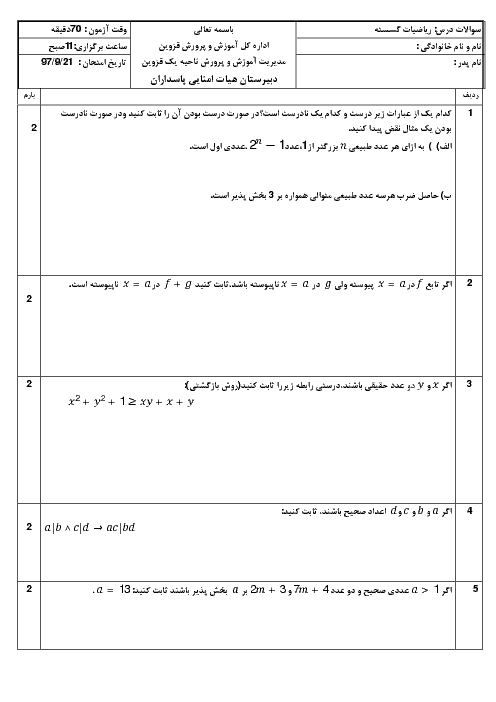
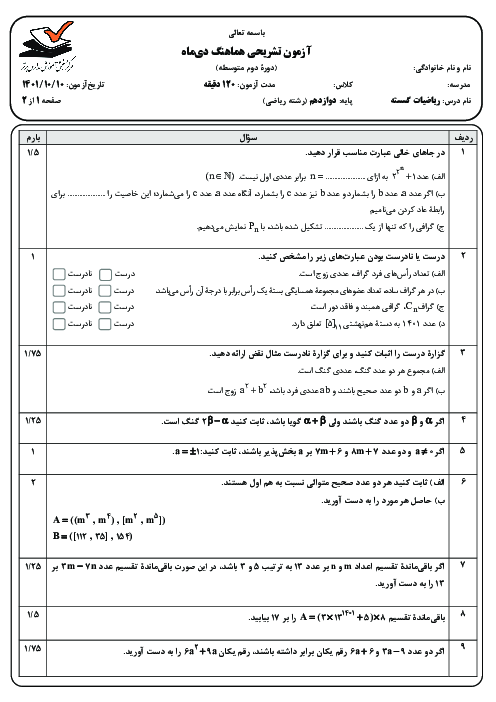
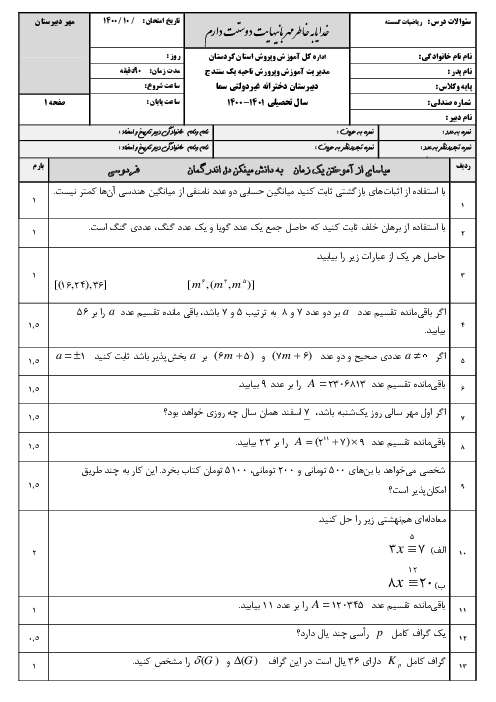
** فصل 1: آشنایی با نظریه اعداد ریاضیات گسسته دوازدهم دوره دوم متوسطه- نظری علوم ریاضی درسنامه آموزشی این مبحث

اگر $a$ مضرب $3$ باشد؛ ولی مضرب $6$ نباشد، آنگاه ${{a}^{2}}$ به كدام‌يك از صورت‌های زير نوشته می‌شود؟

1 )

$4k$

2 )

$4k+1$

3 )

$4k+2$

4 )

$4k+3$

نمایش پاسخ

نکته: اگر $a$ عددی صحیح و $b$ عددی طبيعی باشد، آنگاه اعداد صحيح و منحصربه‌فرد $r$ و $q$ وجود دارد به طوری‌كه $0\le r\langle b,a=bq+r$

با توجه به نكته‌ی بالا، هر عدد مانند $a$ به يكی از شكل‌های زير نوشته می‌شود:

$a=6k,a=6k+1,a=6k+2,a=6k+3,a=6k+4,a=6k+5$

مطابق فرض سؤال $a$ مضرب $3$ است؛ ولی مضرب $6$ نيست، پس فقط $a=6k+3$ قابل قبول است. به‌ازای اين مقدار داريم:

$a=6k+3\Rightarrow {{a}^{2}}=36{{k}^{2}}+36k+9\Rightarrow {{a}^{2}}=4(\underbrace{9{{k}^{2}}+9k+2}_{q})+1=4q+1$

پس باقی‌مانده‌ی تقسيم ${{a}^{2}}$ بر $4$ برابر يك است، يعنی گزينه‌ی ۲ پاسخ است.

گزارش اشکال

یک تست دیگه بزن

یک آزمون کامل بده

تحلیل ویدئویی تست

1401/08/25

محسن ذوالفقاری

پاورپوینت دوره آموزشی، ریاضیات گسسته دوازدهم دوره دوم متوسطه- نظری

مدرس: رضا زینی وند

مدت دوره: 275 اسلاید (10 فایل)

با گنجینه سوال، آزمون دلخواهتو بساز

سوپراستار

بسته ویژه نمره بیست: 18 دوره امتحان نهایی درس گسسته دوازدهم

69 صفحه

بسته ویژه نمره بیست: 18 دوره امتحان نهایی درس گسسته دوازدهم

ويژه نامه نوبت اول و…

سوپراستار

جزوه آموزشی، تمرین و تست ریاضیات گسسته | فصل 3: ترکیبیات

28 صفحه

جزوه آموزشی، تمرین و تست ریاضیات گسسته | فصل 3: ترکیبیات

عاصف محبی

آزمون نوبت اول ریاضیات گسسته دوازدهم دبیرستان غیردولتی اندیشه های شریف | دی 1398

4 صفحه

آزمون نوبت اول ریاضیات گسسته دوازدهم دبیرستان غیردولتی اندیشه های شریف…

محمد احمدزاده

خلاصه درس و گام به گام ریاضیات گسسته فصل 2: گراف و مدلسازی

24 صفحه

خلاصه درس و گام به گام ریاضیات گسسته فصل 2: گراف و مدلسازی

اسدالله رضازاده

امتحان تستی ترم اول ریاضیات گسسته دوازدهم دبیرستان نمونه خیامی قائن | دی 1399

9 صفحه

امتحان تستی ترم اول ریاضیات گسسته دوازدهم دبیرستان نمونه خیامی قائن |…

سیدمسعود حجتی

نمونه سوال آزمون ترم اول دیماه 1403 درس ریاضی گسسته

5 صفحه

نمونه سوال آزمون ترم اول دیماه 1403 درس ریاضی گسسته

مجتبی زمانی

آزمون مستمر ترم اول ریاضیات گسسته: ص. 18 تا 42

4 صفحه

آزمون مستمر ترم اول ریاضیات گسسته: ص. 18 تا 42

اردوان مختاری

حل تشریحی سوالات امتحانات نهایی سال های 1397 تا 1402 درس ریاضیات گسسته | نیمسال اول: ص. 1 تا 42

32 صفحه

حل تشریحی سوالات امتحانات نهایی سال های 1397 تا 1402 درس ریاضیات گسسته…

محمد مدبر

رایـــــگان

سؤالات امتحان نهایی درس ریاضیات گسسته دوازدهم رشته ریاضی | شهریور 1398

5 صفحه

سؤالات امتحان نهایی درس ریاضیات گسسته دوازدهم رشته ریاضی | شهریور 1398

امتحان نهایی

آزمون نوبت اول ریاضیات گسسته دوازدهم ریاضی دبیرستان 17 شهریور | دی ماه 1403 (تا ص. 42)

5 صفحه

آزمون نوبت اول ریاضیات گسسته دوازدهم ریاضی دبیرستان 17 شهریور | دی ماه…

خدیجه اقدامی مقدم

موارد بیشتر

موارد بیشتر

ارسال فایل

عدد صحیح q در بخش پذیری 2 عدد a و b نشان دهنده چیست؟

می‌خواهیم یک گروه 7 نفره را از دو پایه انتخاب کنیم. این کار به چند طریق امکان دارد؛ اگر ملزم باشیم دقیقا 4 دانشجوی سال دوم و5 پسر انتخاب کنیم؟

تعداد درخت‌های مرتبه 6 در ریاضیات گسسته

موارد بیشتر

ارسال پرسش

موارد بیشتر