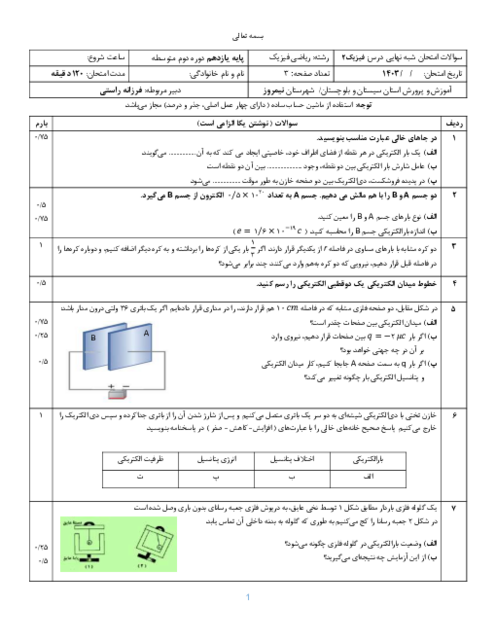
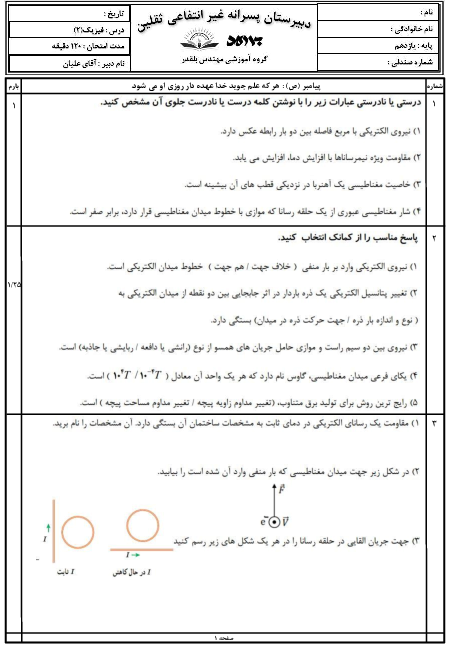
مطابق شکل زیر، سه بار الکتریکی نقطه‌ای در سه رأس مربعی به ضلع ۱ متر ثابت شده اند. بردار برایند میدان های الکتریکی حاصل از این سه بار در رأس C و در SI مطابق کدام گزینه است؟ $k=۹\times {{۱۰}^{۹}}\frac{N.{{m}^{۲}}}{{{C}^{۲}}}$

$\overrightarrow{E}=-۱۸\times {{۱۰}^{۹}}\overrightarrow{i}+۹\times {{۱۰}^{۹}}\overrightarrow{j}$

$\overrightarrow{E}=-۳۶\times {{۱۰}^{۹}}\overrightarrow{i}+۹\times {{۱۰}^{۹}}\overrightarrow{j}$

$\overrightarrow{E}=۳۶\times {{۱۰}^{۹}}\overrightarrow{i}+۱۸\times {{۱۰}^{۹}}\overrightarrow{j}$

$\overrightarrow{E}=-۳۶\times {{۱۰}^{۹}}\overrightarrow{i}+۱۸\times {{۱۰}^{۹}}\overrightarrow{j}$