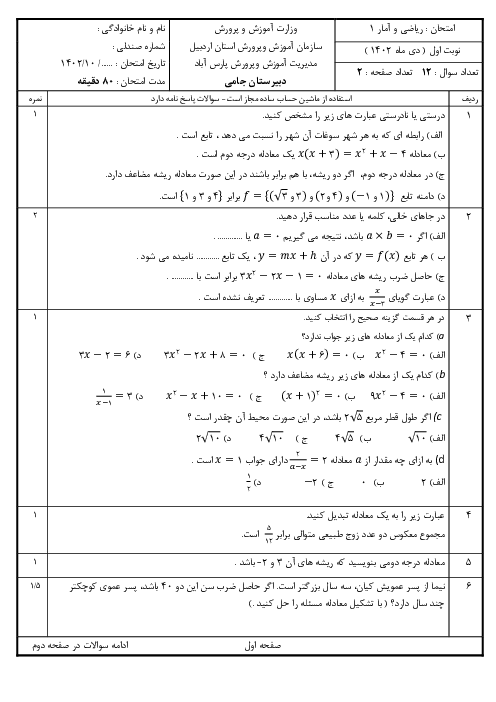
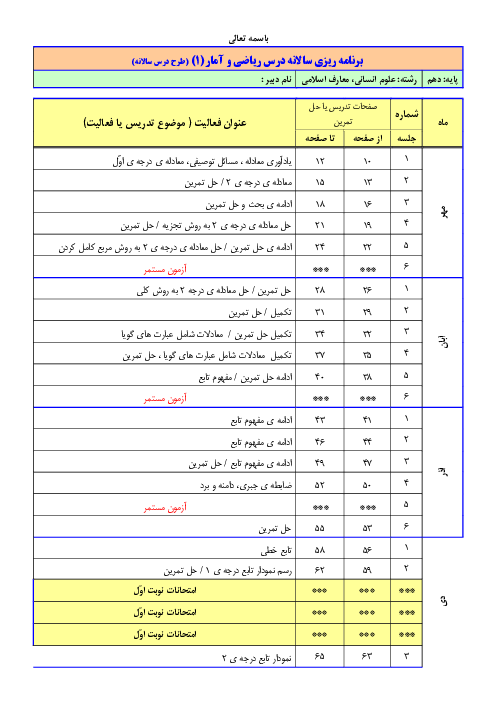
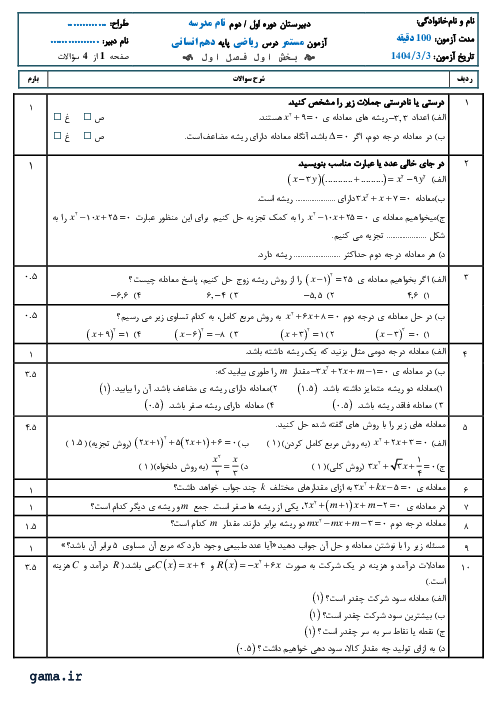
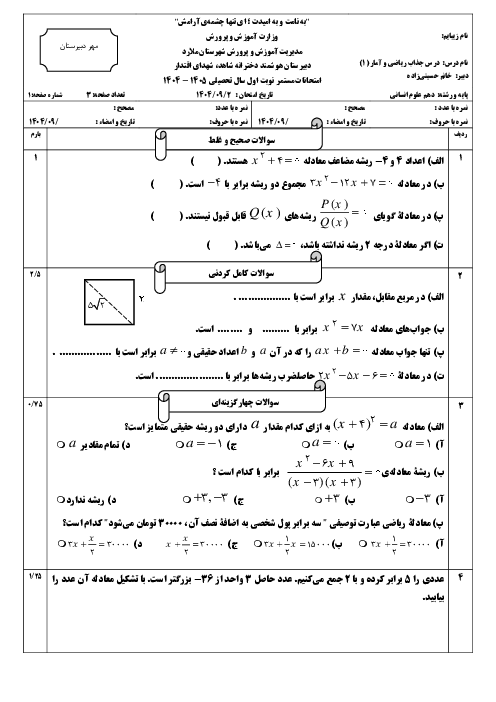
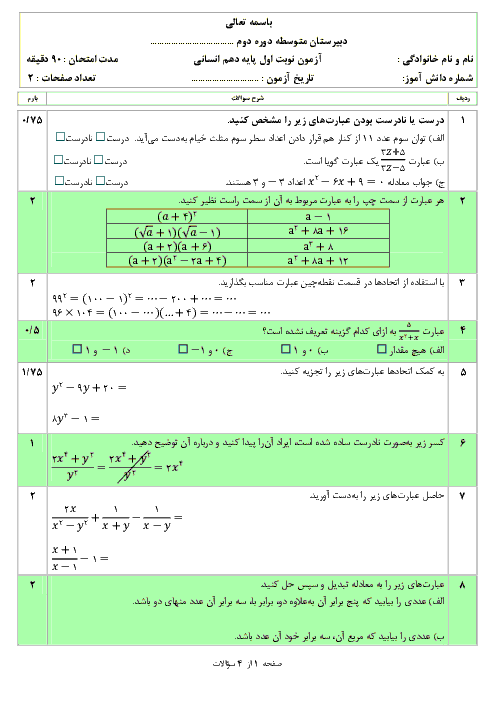
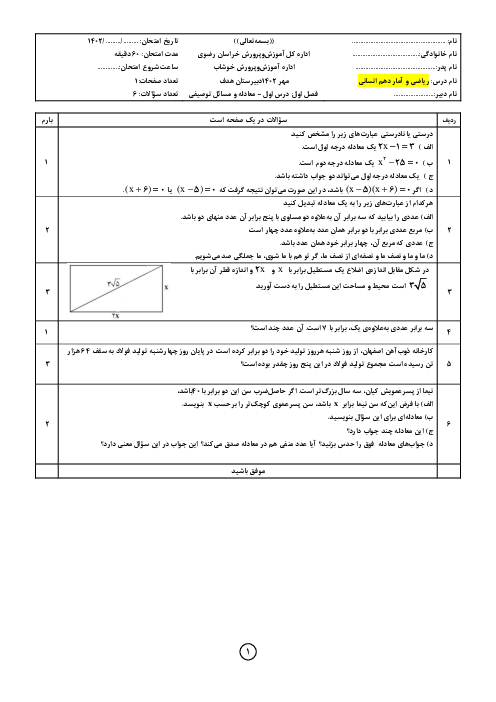
درس 4: رسم تابع درجۀ 2
ریاضی و آمار (1)
دهم
متوسطه دوم نظری
ادبیات و علوم انسانی
درسنامه آموزشی این مبحث
تابع درجهٔ دوم $y = - 2{x^2} + 3x - 5$ و خط $y = - 8x + 9$ در کدام یک از نقاط زیر یک دیگر را قطع میکنند؟
1 )
$( - \frac{7}{2},19)$
2 )
$(\frac{7}{2},19)$
3 )
$( - 2,7)$
$(2, - 7)$
پاسخ تشریحی :
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!