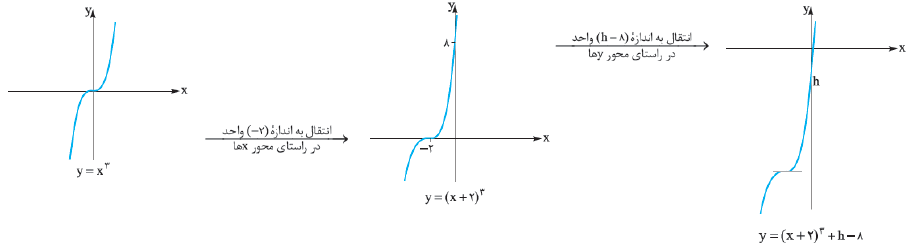
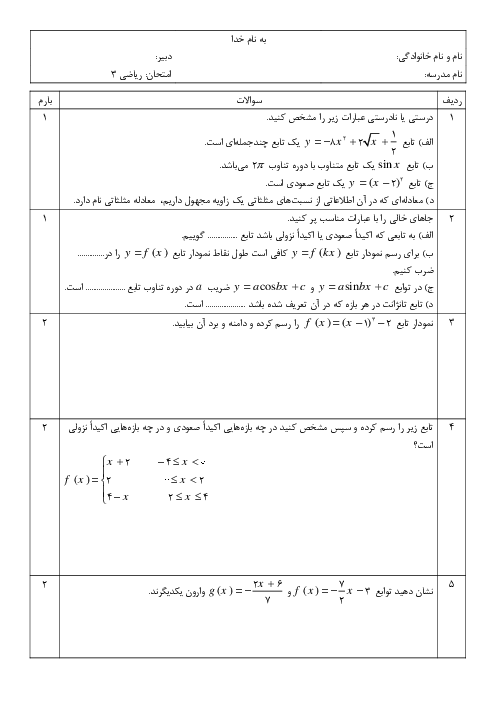
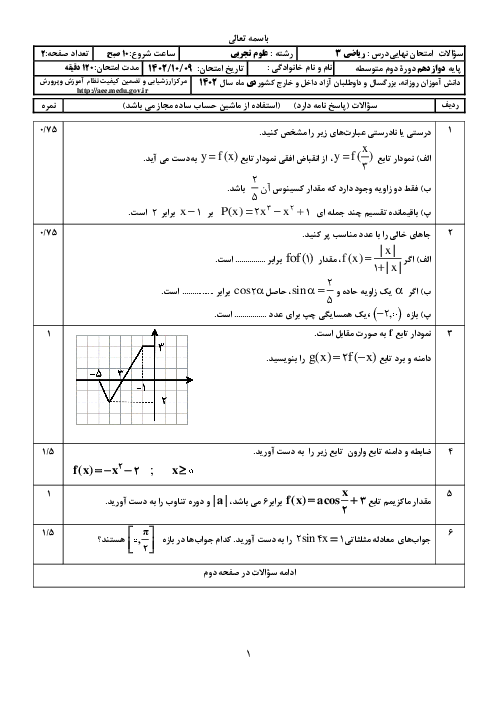
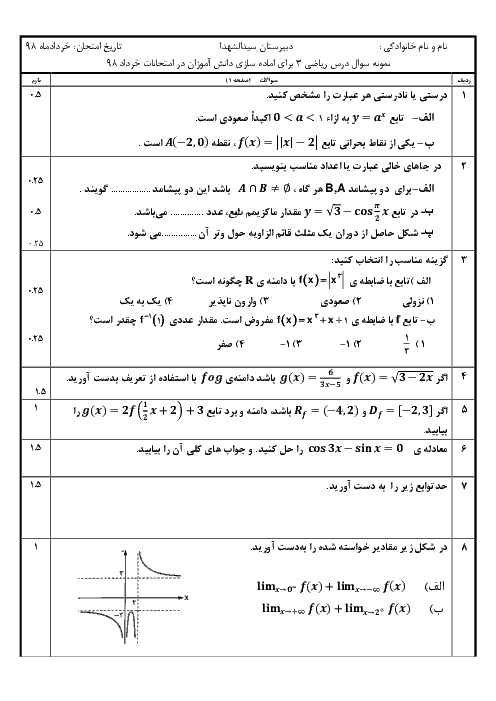
درس 1: توابع چند جمله‌ای- توابع صعودی و نزولی
ریاضی (3)
دوازدهم
دوره دوم متوسطه- نظری
علوم تجربی
درسنامه آموزشی این مبحث
به ازای چه مقادیری از $h$ تابع $f(x)={{x}^{3}}+6{{x}^{2}}+12x+h$ از ربع دوم عبور نمی‌کند؟
تحلیل ویدئویی تست
علیرضا زینی وند 
مهدی خلجی 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...