درس 2: تابع درجه سوم، توابع یکنوا و بخش‌پذیری و تقسیم
حسابان (2)
دوازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
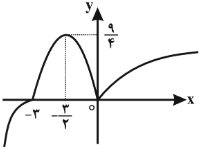
در کدام بازه‌ها، تابع $f(x)=\left\{ \begin{matrix} 2{{(x+3)}^{3}}\begin{matrix}{} \\\end{matrix};\begin{matrix}{} \\\end{matrix}x \lt -3\begin{matrix}{} \\\end{matrix}\begin{matrix}\end{matrix} \\{} \\ -{{x}^{2}}-3x\begin{matrix}{} \\\end{matrix};\begin{matrix}{} \\\end{matrix}-3\le x \lt 0 \\ \sqrt{x}\begin{matrix}{} & {} & {} \\\end{matrix};\begin{matrix}\end{matrix}x\ge 0\begin{matrix}{} \\ {} & {} \\\end{matrix} \\\end{matrix} \right.$، به ترتیب از راست به چپ صعودی و نزولی است؟
1 )
$(-1,+\infty )$ و $(-2,-1)$
2 )
$(-3,-2)$ و $[-1,1]$
$[-4,-2]$ و $[-1,0]$
4 )
$[-2,-1]$ و $\left[ -\frac{3}{2},-1 \right]$
پاسخ تشریحی :
تحلیل ویدئویی تست
عباس ابراهیمی علویجه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...