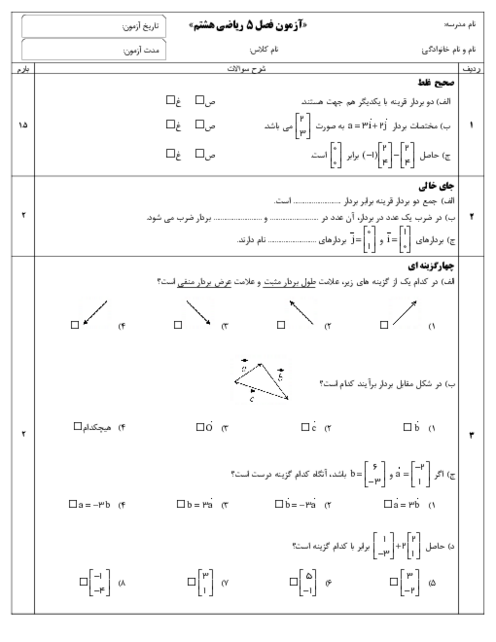
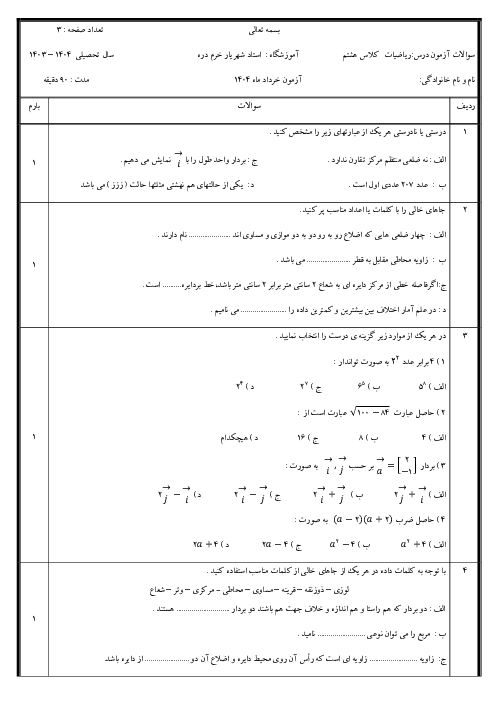
$-2\left[ \begin{matrix}    3  \\    -4  \\ \end{matrix} \right]-3\overrightarrow{x}=\left[ \begin{matrix}    6  \\    -1  \\ \end{matrix} \right]\Rightarrow \left[ \begin{matrix}    -6  \\    8  \\ \end{matrix} \right]-3\overrightarrow{x}=\left[ \begin{matrix}    6  \\    -1  \\ \end{matrix} \right]\xrightarrow{-\left[ \begin{matrix}    -6  \\    8  \\ \end{matrix} \right]}\not{\left[ \begin{matrix}    -6  \\    8  \\ \end{matrix} \right]}-not{\left[ \begin{matrix}    -6  \\    8  \\ \end{matrix} \right]}-3\overrightarrow{x}=\left[ \begin{matrix}    6  \\  -1  \\ \end{matrix} \right]-\left[ \begin{matrix}    -6  \\    8  \\ \end{matrix} \right]$ 

$\Rightarrow -3\overrightarrow{x}=\left[ \begin{matrix}    6  \\    -1  \\ \end{matrix} \right]+\left[ \begin{matrix}    6  \\    -8  \\ \end{matrix} \right]=\left[ \begin{matrix}    12  \\    -9  \\ \end{matrix} \right]\Rightarrow -3\overrightarrow{x}=\left[ \begin{matrix}    12  \\    -9  \\ \end{matrix} \right]\xrightarrow{-3}\frac{-3}{-3}\overrightarrow{x}=\left[ \begin{matrix}    \frac{12}{-3}  \\    \frac{-9}{-3}  \\ \end{matrix} \right]\Rightarrow \overrightarrow{x}=\left[ \begin{matrix}    -4  \\    3  \\ \end{matrix} \right]$