درس 1: توابع چند جمله‌ای- توابع صعودی و نزولی
ریاضی (3)
دوازدهم
دوره دوم متوسطه- نظری
علوم تجربی
درسنامه آموزشی این مبحث
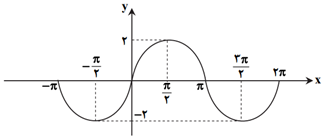
تابع $f(x)=2\operatorname{Sin}x$ در كدام‌يک از بازه‌های زير اكيداً نزولی است؟
1 )
$(0,\frac{\pi }{2})$
2 )
$(\frac{3\pi }{2},2\pi )$
$(\pi ,\frac{3\pi }{2})$
4 )
$(-\frac{\pi }{2},0)$
پاسخ تشریحی :
تحلیل ویدئویی تست
علیرضا زینی وند 
مهدی خلجی 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...