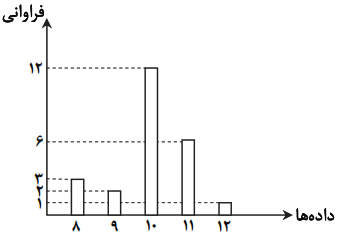
نكته‌ی 1: در نمودار ميله‌اي، محور xها نمايشگر داده‌ها و محور yها نمايشگر فراوانی داده‌ها است.

نكته‌ی 2: ضريب تغييرات داده‌های ${{x}_{1}}$، ${{x}_{2}}$، ${{x}_{3}}$، ... و ${{x}_{n}}$ برابر است با خارج‌قسمت تقسیم انحراف‌معیار داده‌ها $(\sigma )$ بر میانگین داده‌ها $(\overline{x})$ که آن‌را با CV نمایش می‌دهیم:

$CV=\frac{\sigma }{x}$

نکته‌ی 3: میانگین و انحراف‌معیار داده‌های ${{x}_{1}}$، ${{x}_{2}}$، ${{x}_{3}}$، ... و ${{x}_{n}}$ با فراوانی ${{f}_{1}}$، ${{f}_{2}}$، ${{f}_{3}}$، ... و ${{f}_{n}}$ برابر است با:

$\overline{x}=\frac{\sum\limits_{i=1}^{n}{{{f}_{i}}{{x}_{i}}}}{\sum\limits_{i=1}^{n}{{{f}_{i}}}}\,\,\,\,\,\,\,\,\,\,,\,\,\,\,\,\,\,\,\,\,\sigma =\sqrt{\frac{\sum\limits_{i=1}^{n}{{{f}_{i}}?{{({{x}_{i}}-\overline{x})}^{2}}}}{\sum\limits_{i=1}^{n}{{{f}_{i}}}}}$

با توجه به نكات، به‌ترتيب، ميانگين و انحراف‌معيار را محاسبه می‌كنيم تا ضريب تغييرات به‌دست آيد:

$\begin{align}
  & \overline{x}=\frac{(8\times 3)+(9\times 2)+(10\times 12)+(11\times 6)+(12\times 1)}{3+2+12+6+1}=10 \\ 
 & \sigma =\sqrt{\frac{3{{(8-10)}^{2}}+2{{(9-10)}^{2}}+12{{(10-10)}^{2}}+6{{(11-10)}^{2}}+1{{(12-10)}^{2}}}{24}}=1 \\ 
 & CV=\frac{\sigma }{\overline{x}}=\frac{1}{10}=0/1 \\ 
\end{align}$