درس 1: ماتریس و اعمال روی ماتریس‌ها
هندسه (3)
دوازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
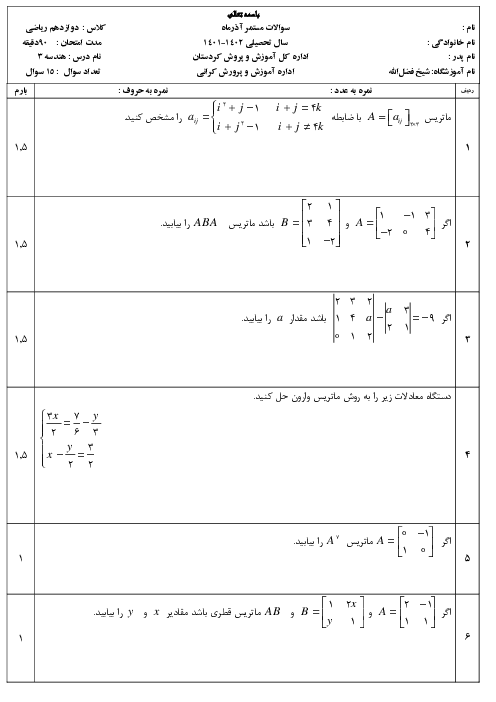
اگر $A={{\left[ {{a}_{ij}} \right]}_{2\times 3}}$ و داشته باشیم ${{a}_{ij}}=\left\{ \begin{matrix} \begin{matrix} 2i+j & i\lt j \\ \end{matrix} \\ \begin{matrix} {{i}^{2}} & i=j \\ \end{matrix} \\ \begin{matrix} j-i & i\gt j \\ \end{matrix} \\ \end{matrix} \right.$ ماتریس $A$ کدام است؟
$\left[ \begin{matrix} \begin{matrix} 1 \\ -1 \\ \end{matrix} & \begin{matrix} 4 \\ 4 \\ \end{matrix} & \begin{matrix} 5 \\ 7 \\ \end{matrix} \\ \end{matrix} \right]$
2 )
$\left[ \begin{matrix} \begin{matrix} 1 & 4 \\ \end{matrix} \\ \begin{matrix} -1 & 4 \\ \end{matrix} \\ \begin{matrix} -2 & -1 \\ \end{matrix} \\ \end{matrix} \right]$
3 )
$\left[ \begin{matrix} \begin{matrix} 1 & -1 \\ \end{matrix} \\ \begin{matrix} 4 & 4 \\ \end{matrix} \\ \begin{matrix} 5 & 7 \\ \end{matrix} \\ \end{matrix} \right]$
4 )
$\left[ \begin{matrix} \begin{matrix} 1 \\ 5 \\ \end{matrix} & \begin{matrix} -1 \\ 4 \\ \end{matrix} & \begin{matrix} 2 \\ 1 \\ \end{matrix} \\ \end{matrix} \right]$
تحلیل ویدئویی تست
ندا تقوی 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...