نکتۀ 1: دامنۀ تابع مرکب gof مجموعه xهایی است که هم‌زمان در دو شرط زیر صدق کنند:

1) x در دامنۀ f قرار داشته باشد.

2) f(x) در دامنۀ g قرار داشته باشد.

${D_{gof}} = \left\{ {x \in \left. {{D_f}} \right|} \right.f(x) \in \left. {{D_g}} \right\}$

نکتۀ 2: اگر برای هر دو نقطۀ ${x_1}$ و ${x_2}$ از مجموعۀ $(A \subseteq {D_f})A$ که ${x_1} \lt {x_2}$ ، داشته باشیم $f({x_1}) \gt f({x_2})$ ، آن‌گاه f را تابعی اکیداً نزولی می‌نامیم.

ابتدا دامنۀ تابع g با ضابطۀ $y = 2\sqrt {1 - x}  - 3$ را پیدا می‌کنیم:

$1 - x \geqslant 0 \Rightarrow x \leqslant 1 \Rightarrow {D_g} = ( - \infty ,\left. 1 \right]$

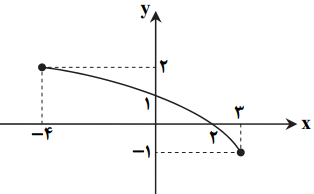
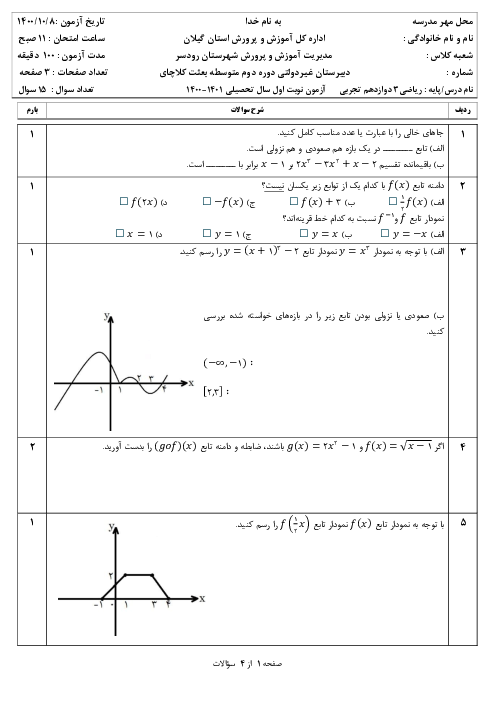
هم‌چنین با توجه به نمودار تابع f داده شده؛ ${D_f} = \left[ { - 4,3} \right]$ ، پس دامنۀ تابع مرکب gof برابر است با:

${D_{gof}} = \left\{ {x \in \left. {{D_f}} \right|f(x) \in {D_g}} \right\} = \left\{ { - 4 \leqslant x \leqslant 3\left| {f(x) \leqslant 1} \right.} \right\}$

برای حال نامعادلۀ $f(x) \leqslant 1$ توجه کنید که $$f(0) = 1$$ و f تابعی اکیداً نزولی است، پس:

$f(x) \leqslant 1 \Rightarrow f(x) \leqslant f(0) \Rightarrow x \geqslant 0$

بنابراین دامنۀ gof برابر است با:

${D_{gof}} = \left\{ { - 4 \leqslant x \leqslant 3\left| {x \geqslant 0} \right.} \right\} = \left[ {0,3} \right]$