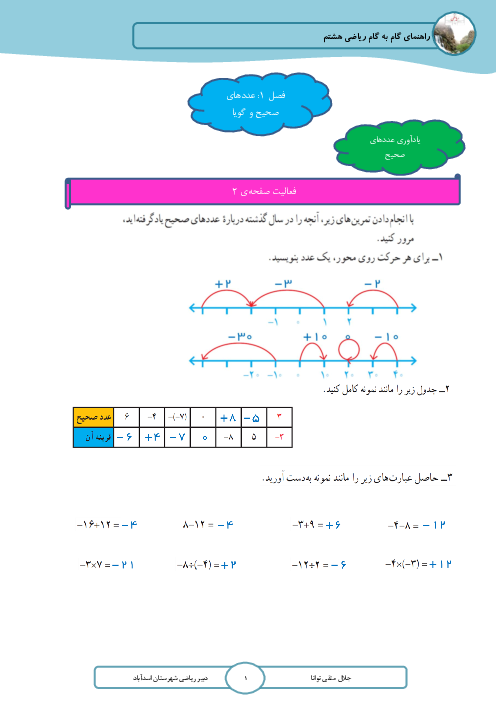
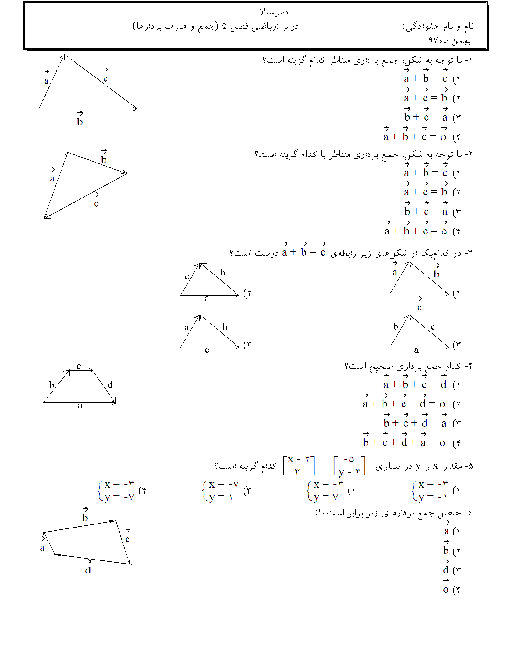
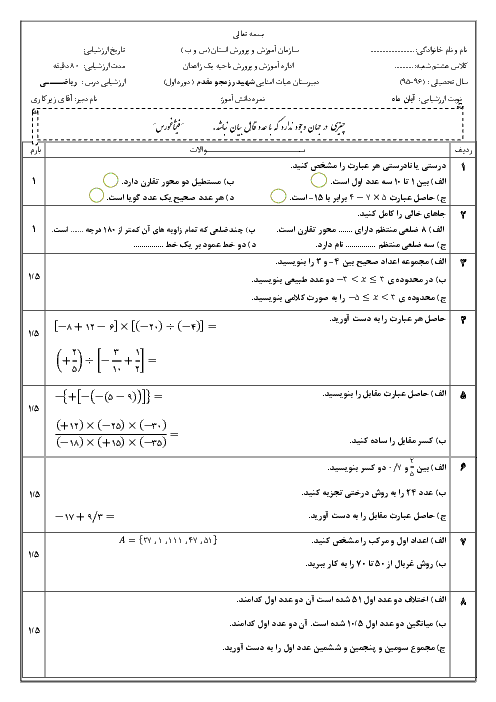
اگر داشته باشیم $\overrightarrow{a}=-2i+j,\overrightarrow{b}=i-\frac{1}{2}j,\overrightarrow{x}=\frac{1}{2}\overrightarrow{a}-\overrightarrow{2b}$ و مقدار عددی بردار $\overrightarrow{x}$ کدام است؟
1 )
$\left[ \begin{matrix} -1 \\ \frac{1}{3} \\ \end{matrix} \right]$
$\left[ \begin{matrix} -3 \\ \frac{3}{2} \\ \end{matrix} \right]$
3 )
$\left[ \begin{matrix} -2 \\ 1 \\ \end{matrix} \right]$
4 )
$\left[ \begin{matrix} 1 \\ -\frac{1}{1} \\ \end{matrix} \right]$
پاسخ تشریحی :
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...