درس 2: تابع درجه سوم، توابع یکنوا و بخش‌پذیری و تقسیم
حسابان (2)
دوازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
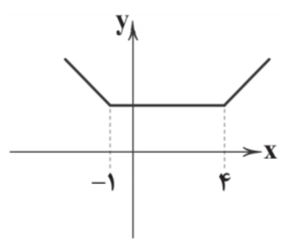
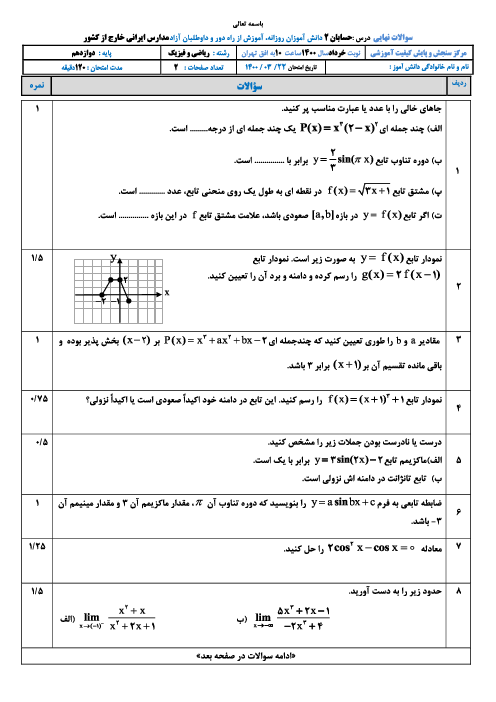
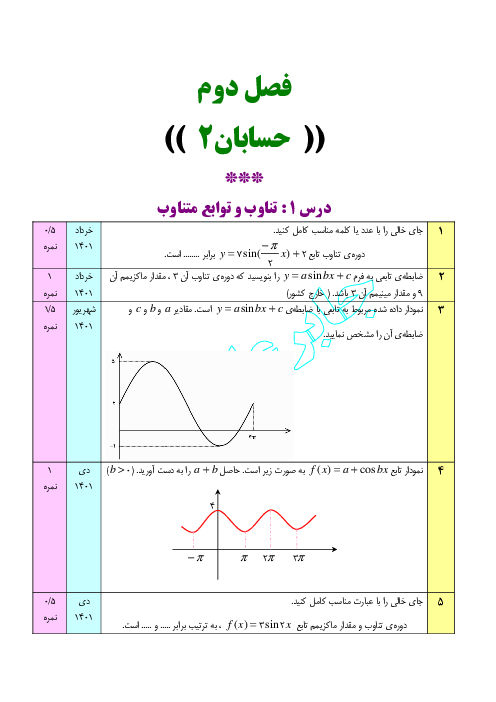
تابع $f(x)=\left| x+1 \right|+\left| x-a \right|$ در فاصلهٔ $\left[ -1\,\,,\,\,4 \right]$ ثابت است. بزرگ‌ترین بازه‌ای که تابع در آن صعودی است، کدام است؟
1 )
$\left[ 4\,\,,\,\,+\infty \right)$
2 )
$[-2\,\,,\,\,4]$
3 )
$\left[ -2\,\,,\,\,+\infty \right)$
$\left[ -1\,\,,\,\,+\infty \right)$
پاسخ تشریحی :
تحلیل ویدئویی تست
عباس ابراهیمی علویجه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...