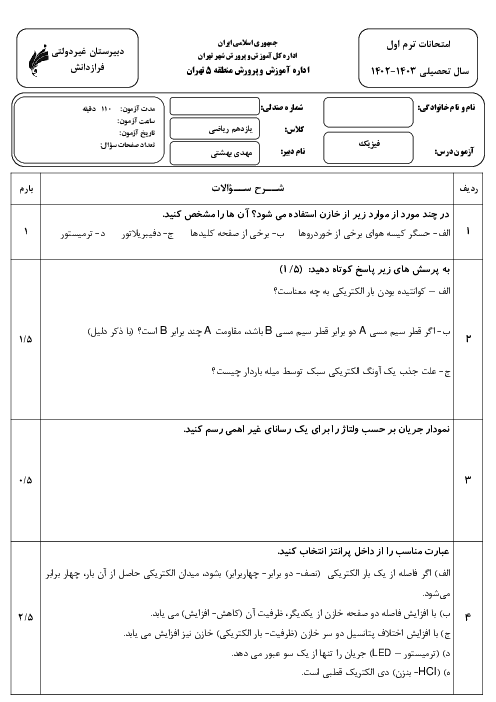
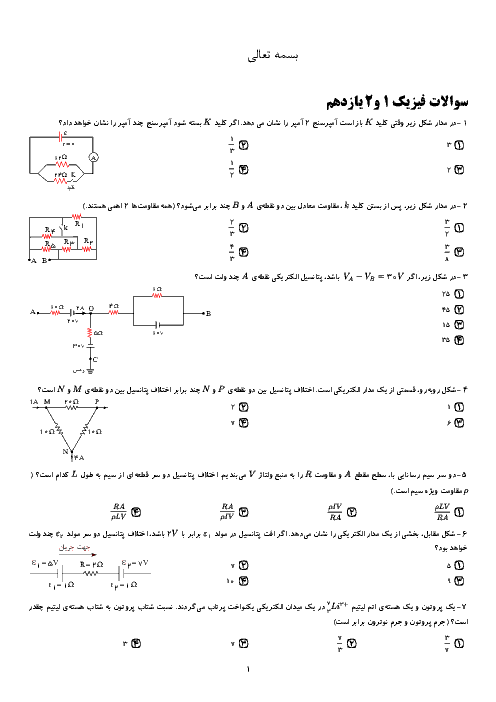
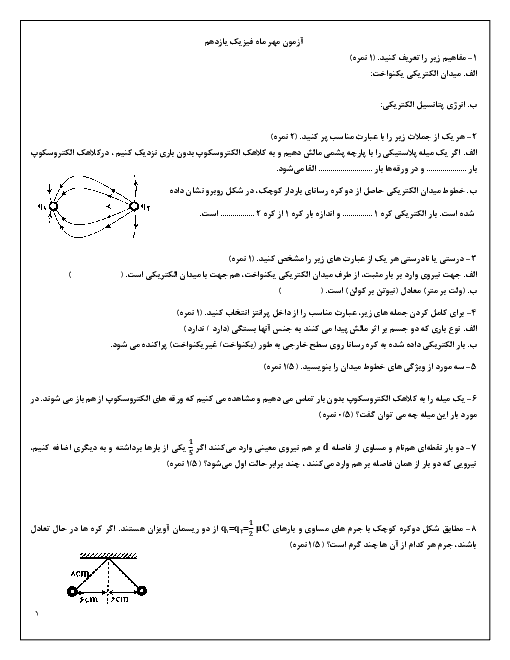
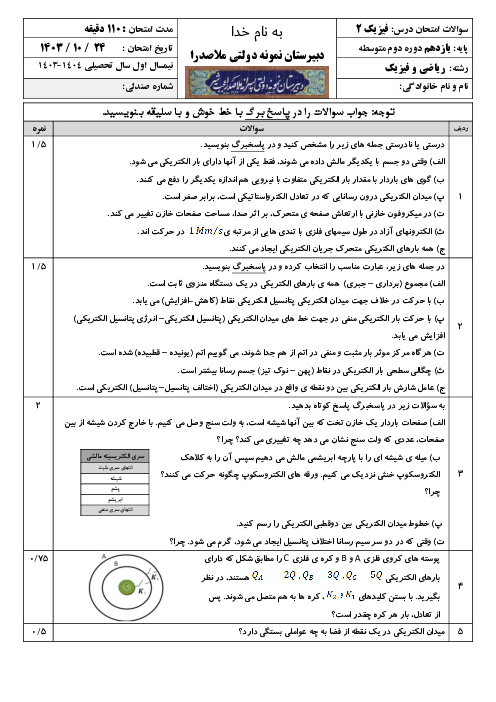
ابتدا تغيير مقدار مقاومت رشتهٔ درون لامپ را حساب می‌كنيم و سپس از رابطهٔ $P=\frac{{{V}^{2}}}{R}$، تغییر توان آن را به‌دست می‌آوریم:

${{R}_{2}}={{R}_{1}}(1+\alpha \Delta \theta )\xrightarrow{\Delta \theta ={{2250}^{{}^\circ }}C,\alpha =4\times {{10}^{-3}}\frac{1}{{}^{{}^\circ }C}}$

${{R}_{2}}={{R}_{1}}(1+4\times {{10}^{-3}}\times 2250)\Rightarrow {{R}_{2}}=10{{R}_{1}}$

$P=\frac{{{V}^{2}}}{R}\xrightarrow{{{V}_{1}}={{V}_{2}}}\frac{{{P}_{2}}}{{{P}_{1}}}=\frac{{{R}_{1}}}{{{R}_{2}}}\xrightarrow{{{R}_{2}}=10{{R}_{1}}}$

$\frac{{{P}_{2}}}{{{P}_{1}}}=\frac{{{R}_{1}}}{10{{R}_{1}}}\Rightarrow \frac{{{P}_{2}}}{{{P}_{1}}}=0/1\Rightarrow {{P}_{2}}=0/1{{P}_{1}}$

$\Delta P={{P}_{2}}-{{P}_{1}}=0/1{{P}_{1}}-{{P}_{1}}\Rightarrow \Delta P=-0/9{{P}_{1}}$

$\frac{\Delta P}{{{P}_{1}}}\times 100=-0/9\times 100=-90%$

پس توان مصرفی لامپ 90 درصد كاهش می‌یابد.